M1 Mathematics, 2011-2012
MM26E Numerical Approximation of PDEs
Hervé Le Dret
$Q_1$-Lagrange approximation
Views of the graph of the shape function for $Q_1$-Lagrange interpolation: $(x_1,x_2)\mapsto x_1x_2$ on the unit square $[0,1]^2$. The affine character of the shape function on segments parallel to the coordinate axes is displayed in magenta:
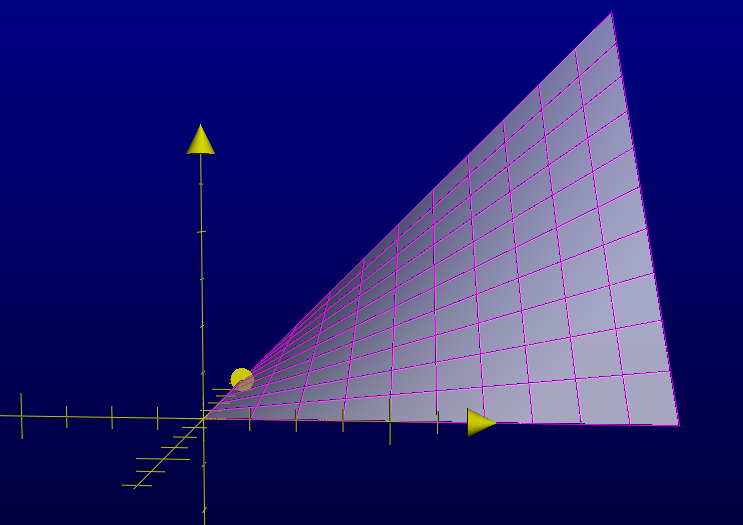
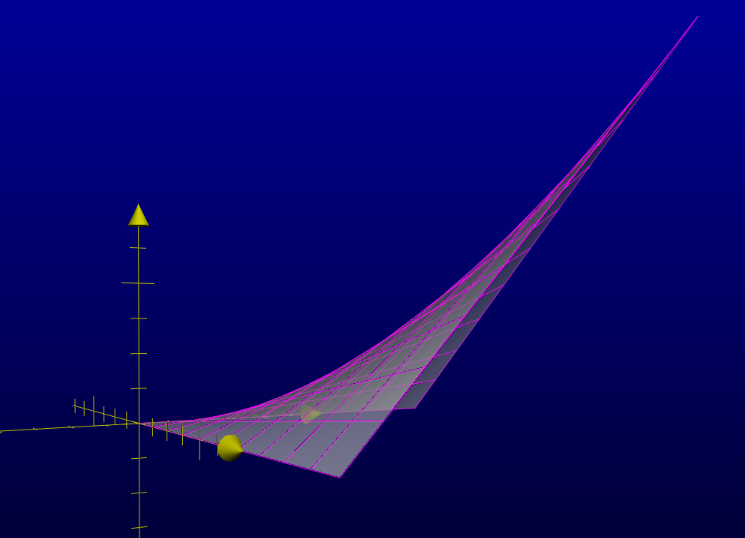
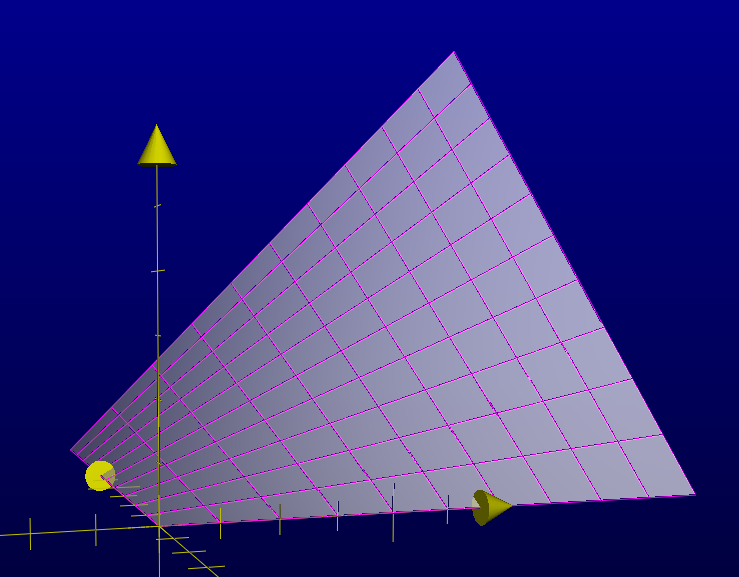
A basis function (hat-function) for $Q_1$-Lagrange interpolation corresponding to an interior node, constructed by patching four copies of the shape function together on the rectangles around the node in question, and extending by zero to the rest of the domain:

A random element of the space $V_h$:

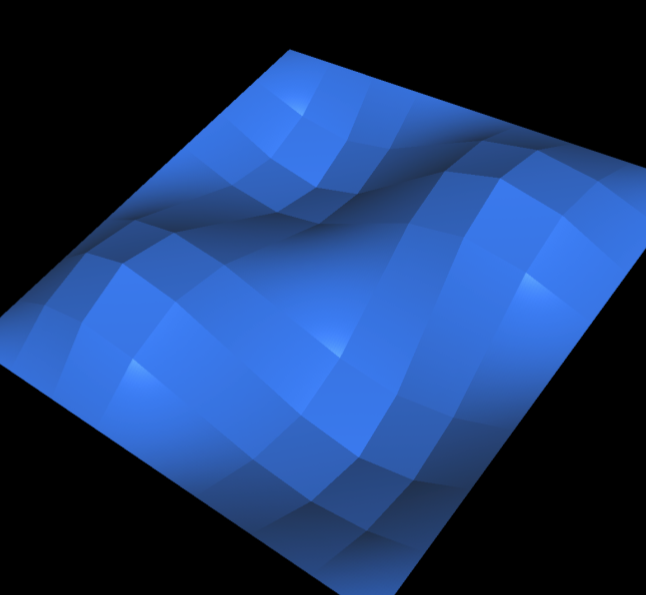
The $V_h$-interpolate of a smooth function $(x_1,x_2)\mapsto \sin x_1 \cos x_2$:
|