M1 Mathematics, 2011-2012
MM26E Numerical Approximation of PDEs
Hervé Le Dret
$Q_2$-Lagrange approximation
Below are the graphs of various basis polynomials of $Q_2$-Lagrange interpolation on the unit square $[0,1]^2$.
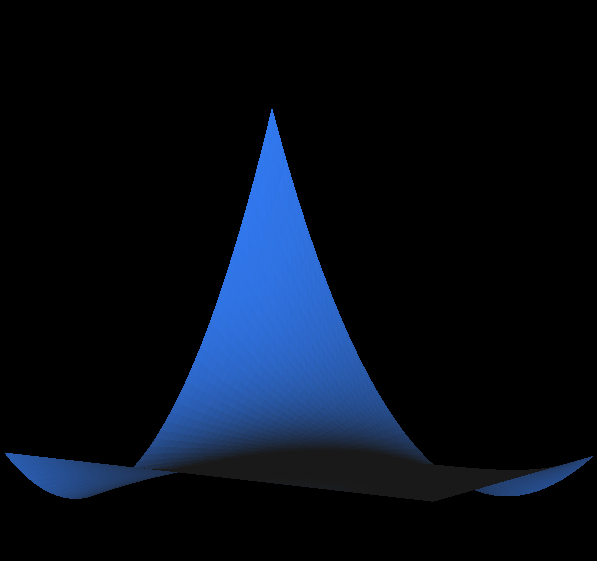
A $Q_2$-shape function interpolating the value 1 at a corner of the square, and with value zero at the other eight nodes, for instance $(x_1,x_2)\mapsto (1-x_1)(1-2x_1)(1-x_2)(1-2x_2)$.
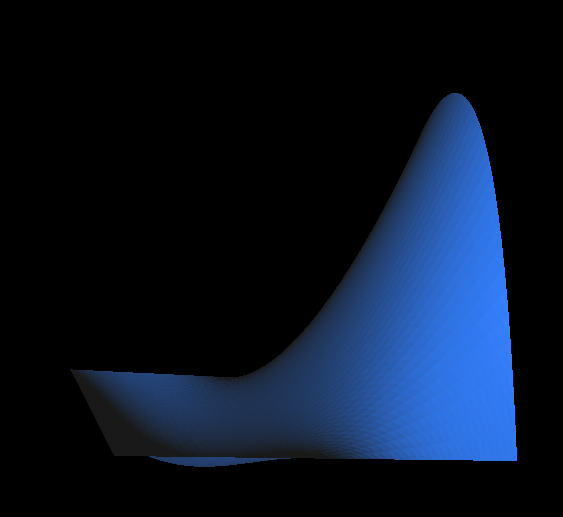
A $Q_2$-shape function interpolating the value 1 at the middle of an edge, and with value zero at the other eight nodes, for instance $(x_1,x_2)\mapsto 4x_1(1-x_1)(1-x_2)(1-2x_2)$.
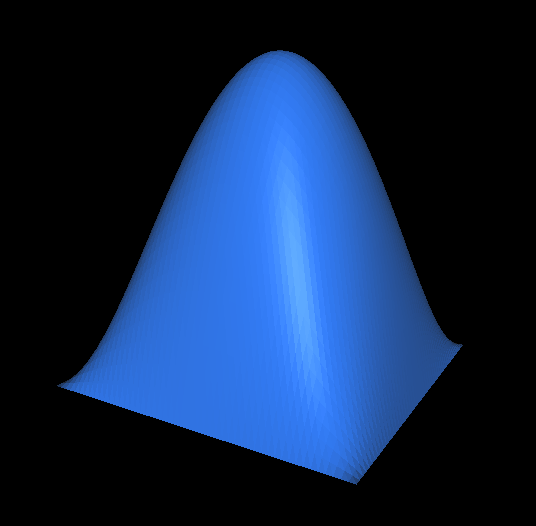
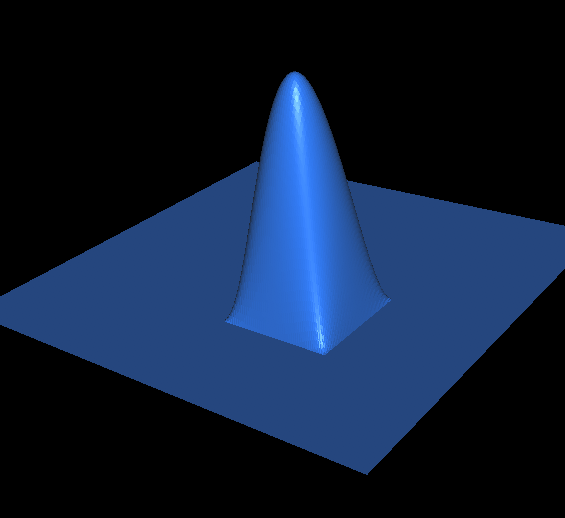
The $Q_2$-shape function interpolating the value 1 at the center of the square, and with value zero at the other eight nodes. It is in particular identically 0 on the boundary of the square, hence the "bubble" name, $(x_1,x_2)\mapsto 16x_1x_2(1-x_1)(1-x_2)$.
Note that the first two kinds of shape functions change sign in the square, which does not happen in the $Q_1$ case.
Below are the hat functions corresponding to the three kinds of shape functions.
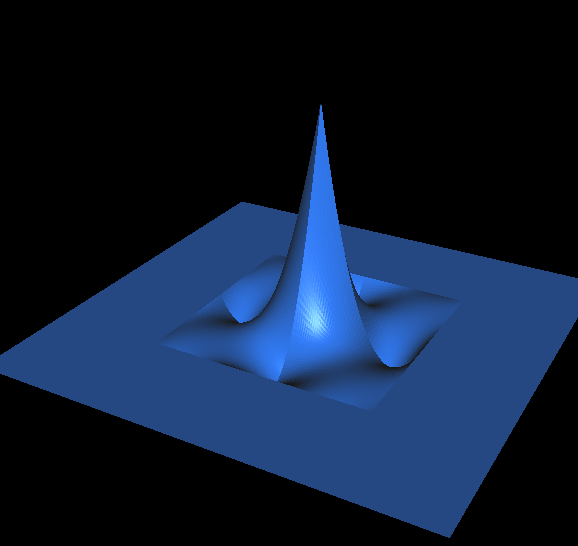

|