Selection of Homework Questions

   

Topic 6: Theory I : Disks

1. Derive the radial oscillation frequency, , for a star perturbed from a circular orbit in an arbitrary axisymmetric potential (R). Express your result first in terms of the angular velocity, (R), and then in terms of the rotation curve, V(R).

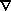2. Show that a disk in which the angular momentum (per unit mass) decreases outwards cannot support stable circular rotation. [Hint: find the condition that perturbations to circular motion cannot yield small epicyclic oscillations.]   (B&T-2 Q 3.8)

3. Starting with Poisson's equation in cylindrical coordinates: ² = 4 G (see B&T-2 Eq B.52 p 777), show that an axisymmetric galaxy has epicycle, vertical and orbital frequencies which obey: ² + ² - 2 ² = 4 G .

4. Use solar neighborhood values for , , and , to estimate the local density in the MW disk. (Adapted from B&T-2 Q 3.15).

(2) Solar Epicyclic Motion :

For the sun, assume a current galactocentric distance R = 8.5 kpc; Oort's constants A = 15 km/s/kpc and B = -12 km/s/kpc; and a current solar motion relative to the local circular velocity of V_r = -10 km/s (ie towards the galactic center) and V = +5.2 km/s (ie faster than circular).

1. Using the epicycle approximation, what are the Sun's minimum and maximum distances from the Galactic center?

2. Assuming the Sun currently resides in the plane and has V_z = 7 km/s, what is the maximum excursion above and below the plane (assume a local mass density of 0.2 M pc^-3, which extends well above the excursion height).

(3) Disk Resonances :

1. Use psm units (Topic 1.3e) to quickly show that a velocity gradient of km/s/kpc has associated angular velocity radians/Gyr, frequency /2 Gyr^-1, and period P = 2 / Gyr.

2. Consider circular orbital motion of angular velocity viewed in a frame rotating with angular velocity F (same, CCW, direction). What is the apparent angular velocity and period of the star? Now add retrograde epicyclic motion of angular velocity . For what values of F does the new orbit appear closed after one revolution? Sketch (or write a program to plot) the shape of the orbit and the guiding circle as seen from the rotating frame when F is:
   1. -
   2. - ½
   3. - ¹/₃
   4. + ½
   5. - 0.49
   Consider a three armed spiral with pattern angular velocity _p = - ¹/₃ . How does the star's epicyclic motion interact with the pattern?

3. A galaxy has the following rotation curve:
   V_c = 200 sin(/2 × R_kpc/2) km/s, 0 < R < 2 kpc
   V_c = 200 km/s, R > 2 kpc.
   The galaxy has a bar and spiral pattern which have constant slow angular velocity of 20 km/s/kpc.

   On a single plot, show and label clearly the following functions of R:   ;   - ½;   + ½;   _p. On the same plot with the same x-axis (but with different y-axis), show the rotation curve, V(R). [Hint: it is easiest to evaluate (R) numerically rather than algebraically].

4. Identify, if present, the locations of the ILR, CR and OLR resonances.

(4) Estimating Pattern Speeds : Express all frequencies in km/s/kpc, and in Myr^-1

1. For a galaxy with a flat rotation curve at 250 km/s, what's the epicyclic frequency at R = 7 kpc?

2. If corotation is at R = 6 kpc, what's this galaxy's pattern speed ?

3. For a two-armed spiral, is R = 7 kpc a resonance radius ?

4. Assume the outer Lindblad resonance is at R = 20 kpc. What's the galaxy's pattern speed now (assume the pattern has m = 2) ?

(5) Disk Stability :

1. Derive an approximate expression for local disk instability to gravitational clumping, the so-called Toomre Q parameter (for stars).

2. A galaxy has rotation curve V = 200 × sin(/2 × R_kpc/3) out to 3 kpc, and is flat (V = 200 km/s) beyond. The disk itself has an exponential scale length of 3 kpc, and surface mass density of 100 M pc^-2 at 6 kpc. Assume the disk has uniform velocity dispersion = 20 km/s and uniform M/L ratio (i.e. the surface density is also exponential).

   Plot a graph of Q vs R to find which parts of the disk are locally unstable (it is probably easiest to evaluate Q numerically).

3. If the disk is "heated" by the passage of orbiting satellites, what is the minimum value of that will supress local instabilities (and associated star formation) throughout the disk?