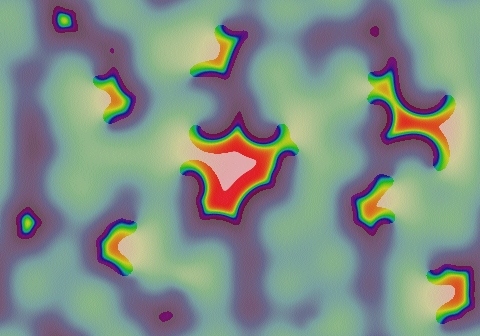
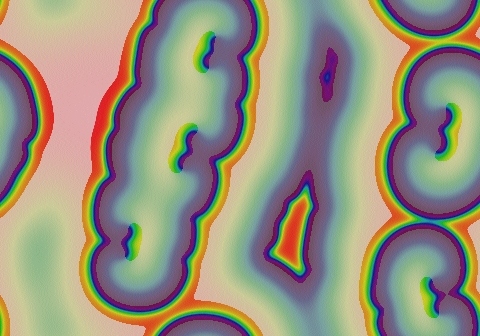
Gray-Scott Model at F 0.0060, k 0.0370

These images and movie demonstrate the behavior of the Gray-Scott reaction-diffusion system with σ=D_u/D_v=2 and parameters F=0.0060, k=0.0370.

Fairly smooth wavefronts, sustained by double-spiral seeds. Note that pairs of spiral seeds tend to move towards each other and annihilate when they meet. By 0:55 in the movie there is only one pair left.

We also see frequent irregularies and occasional breaks in the wavefronts; these breaks occasionaly give rise to new spiral-seed pairs, as seen at 1:38 in the movie in the upper-left area. Such events always occur near a spiral seed and give rise to a new pair (for a total of three spiral seeds). Two of these soon annihilate leaving one remaining seed, usually in a different location. Because these events can cause widely-spaced pairs to drift together, the net effect is towards an overall reduction in seed population. This pattern dies out after another 5,000 tu. A widely spaced pair, in a suitably large domain, can last much longer. A pair separated by 1.8 lu in a 4 lu × 4 lu domain survived for about 200,000 tu.

Categories: Pearson ξ; Wolfram 3 (glossary of terms)

	increase F
decrease k	15 frames/sec.; each fr. is 19 iter. steps = 9.5 tu; 1801 fr. total (17,109 tu)	increase k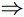

(Click on any image to magnify)

In these images:

Color indicates level of u, ranging from purple (lowest u values) through blue, aqua, green, yellow and pink/red (highest u values)
Areas where u is increasing are lightened to a light pastel tone; where u is decreasing the color is vivid.
In areas where u is changing by less than ±3×10^-6 per tu, an intermediate pastel color is seen. This includes areas that are in steady state or equilibrium.

Wavefronts and other moving objects have decreasing u values (brighter color) on the leading edge of the blue part of the moving object, and increasing u (light pastel color) on the trailing edge. This is true even for very slow-moving objects — thus, you can tell from the coloring what direction things are moving in.

''tu'' is the dimensionless unit of time, and ''lu'' the dimensionless unit of length, implicit in the equations that define the reaction-diffusion model. The grids for these simulations use Δx=1/143 lu and Δt=1/2 tu; the system is 3.2 lu wide. The simulation meets itself at the edges (periodic boundary condition); all images tile seamlessly if used as wallpaper.

Go back to Gray-Scott pattern index

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2019 Jan 05.

s.11