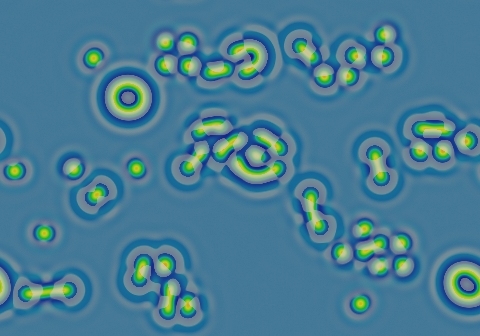
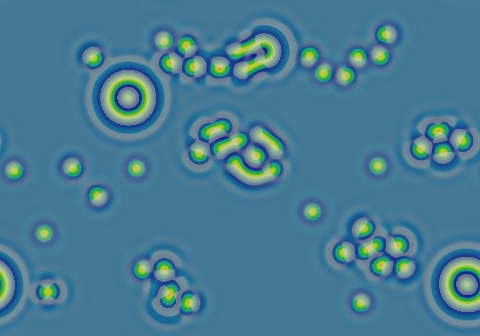
Gray-Scott Model at F 0.0620, k 0.0610

These images and movie demonstrate the behavior of the Gray-Scott reaction-diffusion system with σ=D_u/D_v=2 and parameters F=0.0620, k=0.0610.

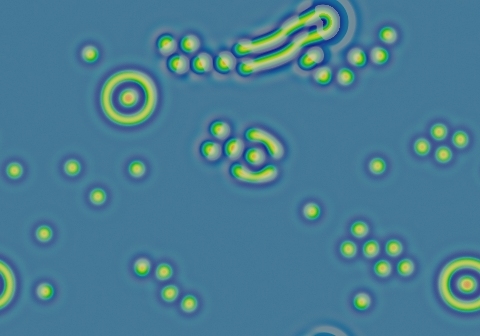
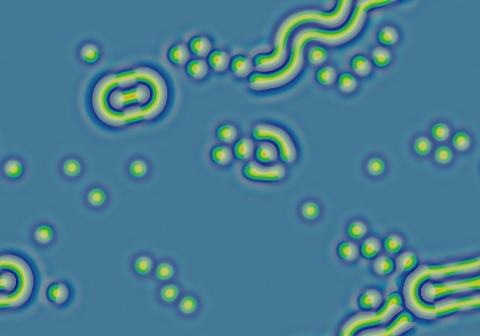
All starting patterns quickly develop into a field of blue with negative solitons (which quickly evolve into true negatons) and negative worms. Sole negatons are possible although chains and hexagonal clumps account for most of the population.

Unlike their positive counterparts, the negative solitons do not yield their position; instead, the surrounding loop connects with whatever was approaching it.

Worms grow slowly, clearing out the space by pushing their surrounding negative bend ahead of them; these will follow the boundaries of the bullseye patterns to form multiple concentric rings.

The symmetrical "bullseye" type pattern seen here is also fairly common. As seen here, it grows very slowly into an elongated double loop; when given enough time and space it lengthens indefinitely. There are many stable patterns (including static, rotating, and continuously moving) at the nearby parameters F=0.0620, k=0.0609.

Bends occasionally bud off new worms. Over the course of 500,000 tu or longer, the space will become filled with the loops and worms, resulting in a fingerprint-like pattern with negative solitons intact.

Categories: Pearson π (borderline); Wolfram 4

The phenomena seen at these parameter values is among the most complex seen in any reaction-diffusion system. There are more images and movies on the uskate world page. (glossary of terms)

		increase F
		15 frames/sec.; each fr. is 159 iter. steps = 79.5 tu; 1800 fr. total (143,100 tu)	increase k

		decrease F

(Click on any image to magnify)

In these images:

Color indicates level of u, ranging from purple (lowest u values) through blue, aqua, green, yellow and pink/red (highest u values)
Areas where u is increasing are lightened to a light pastel tone; where u is decreasing the color is vivid.
In areas where u is changing by less than ±3×10^-6 per tu, an intermediate pastel color is seen. This includes areas that are in steady state or equilibrium.

Wavefronts and other moving objects have decreasing u values (brighter color) on the leading edge of the blue part of the moving object, and increasing u (light pastel color) on the trailing edge. This is true even for very slow-moving objects — thus, you can tell from the coloring what direction things are moving in.

''tu'' is the dimensionless unit of time, and ''lu'' the dimensionless unit of length, implicit in the equations that define the reaction-diffusion model. The grids for these simulations use Δx=1/143 lu and Δt=1/2 tu; the system is 3.2 lu wide. The simulation meets itself at the edges (periodic boundary condition); all images tile seamlessly if used as wallpaper.

Go back to Gray-Scott pattern index

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2019 Jan 05.

s.11