Whittle : EXTRAGALACTIC ASTRONOMY




8. STELLAR DYNAMICS II : 3-D SYSTEMS


(1) Introduction
We have, of course, already begun our study of Stellar Dynamics :
Topic 6 considered the highly
restricted situation of nearly circular motion in cool galaxy disks.
Here we broaden the discussion considerably to consider motion within more
general 3-D systems.
In large part, these notes follow (though simplify) the treatment in B&T.
(a) Gas/Fluid Physics and Stellar Dynamics
To set the stage, lets first compare stellar systems with atomic
(or molecular) gases:
[movies]
(b) A Path Through the Subject
There are a number of themes to cover, and chosing the right sequence isn't
straightforward
Here is an outline to help navigate the upcoming (sometimes dense) material.



(2) Potential Theory
(a) Preliminaries
- We initially characterize mass distributions as smooth functions
 (r)
(r)
(this is usually legitimate for galaxies, see § 8.10 below)
- The gravitational potential energy is a scalar field
its gradient gives the net gravitational force (per unit mass)
which is a vector field :
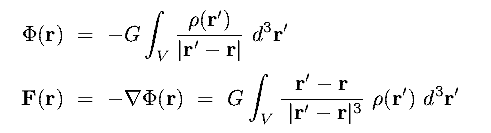 |
(8.1a) (8.1b) |
- evaluating the divergence of F(r) gives :
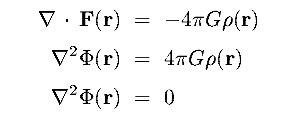 |
(8.2a) (8.2b) (8.2c) |
8.2b is Poisson's equation, for locations within the mass distribution
8.2c is Laplace's equation, for locations outside the mass distribution
- For a volume V with surface A enclosing mass M we have
(using Divergence/Gauss's Theorem) :
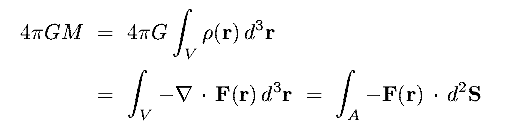 |
(8.3a) (8.3b) |
- Since the force field is the gradient of a potential, it
is conservative,
ie the energy required to move mass from
r1 to r2 is independent of the path
the total Potential Energy is therefore well defined
setting  = 0 at r =
= 0 at r =  we
get (B&T-2 p 59) :
we
get (B&T-2 p 59) :
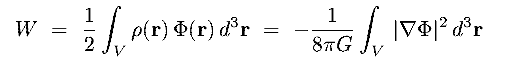 |
(8.4) |
Note that, with this definition, potential energy is always negative
(b) Selected Examples of Density-Potential Pairs
Often, choosing a simple form for  (r)
[or
(r)
[or  (r)] yields a complex form for
(r)] yields a complex form for
 (r)
[or
(r)
[or  (r)]
(r)]
There are, however, a number of useful illustrative analytic
 (r)
(r) 
 (r) pairs :
(r) pairs :
(i) Point Mass
 (r) = - GM / r ; F(r) = -
(r) = - GM / r ; F(r) = -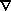
 = -d
= -d /dr = -GM / r2
/dr = -GM / r2
Vc2(r) = GM / r = -  (r) ;
Vesc2(r) = 2GM / r = - 2
(r) ;
Vesc2(r) = 2GM / r = - 2 (r)
(r)
where Vc & Vesc are the circular and escape velocities,
respectively.
This is called a Keplerian Potential, since it pertains
to the solar system.
(ii) Uniform Spherical Shell
Outside :  (r) = - GM / r (Keplerian)
(r) = - GM / r (Keplerian)
Inside :  (r) = const ; F(r) = 0
(r) = const ; F(r) = 0
(iii) Homogeneous Sphere
Sphere radius = a, with  (r) = const (r < a)
(r) = const (r < a)
Outside :  (r) = - GM / r (Keplerian)
(r) = - GM / r (Keplerian)
Inside :  (r) = -2
(r) = -2 G
G (a2 - r2/3) ;
Fr = -G M(r) / r2 = -(4/3)
(a2 - r2/3) ;
Fr = -G M(r) / r2 = -(4/3) G
G  × r
× r
which gives SHM with period Pr = (3 / G
/ G )½ and free-fall tff ~ ¼ Pr ~ (G
)½ and free-fall tff ~ ¼ Pr ~ (G )-½
)-½
Vc =
[(4/3) G
G ]½ × r so that
]½ × r so that  (r) = const
(r) = const
 solid body rotation
solid body rotation
note also that Pc = Pr
(iv) Logarithmic Potentials from Flat Rotation Curves
Many rotation curves are flat at large radii : Vc = Vo, so we have :
 |
(8.5) |
(v) Spherical Systems
- Power Laws :
 =
=
 o (r/a)-
o (r/a)-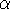
have M(<r) = (4  G a3
G a3  o) / (3 -
o) / (3 - 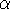 ) × (r / a)3-
) × (r / a)3-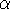
and  (r) = -(4
(r) = -(4  G a2
G a2  o) / [(3 -
o) / [(3 - 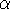 )(
)(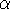 - 2)] × (r / a)2-
- 2)] × (r / a)2-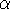 = Vc2 / (
= Vc2 / (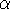 - 2)
- 2)
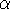 = 3 is a break point:
= 3 is a break point:
For 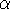 > 3, M(<r)
> 3, M(<r) 
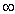 for r
for r  0 : we have infinite mass at the origin.
0 : we have infinite mass at the origin.
For 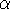 < 3,
M(<r)
< 3,
M(<r) 
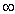 for
r
for
r 
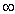 : mass diverges at large r.
: mass diverges at large r.
However for 2 < 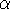 < 3 the potential is finite, as are Vc and Vesc, at all radii.
< 3 the potential is finite, as are Vc and Vesc, at all radii.
The case 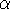 = 2 is special : it is the
singular isothermal sphere
= 2 is special : it is the
singular isothermal sphere
with Vc = (4  G a2
G a2  o)½ = const at all radii, yielding
o)½ = const at all radii, yielding  (r) = 4
(r) = 4  G
a2
G
a2
 o ln(r / a)
o ln(r / a)
See § 8.8a,b,c for other isothermal and related (King) spheres
[link]
- Hernquist (1990) and Jaffe (1983) models: have

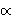 r-4 at large r
r-4 at large r
which fits E gals well, and is theoretically grounded in violent relaxation
at small r, Jaffe core is steeper than Hernquist core :
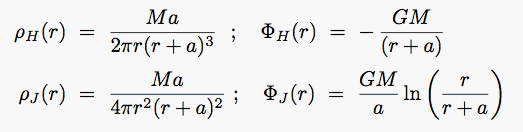 |
(8.6a) (8.6b) |
- Plummer (1911) Sphere: is analytic solution of hydrostatic support for
polytropic stellar system of index 5; see § 8.8a : [link]
 (r) matches GCs well, but is too steep
at large r for Ellipticals (
(r) matches GCs well, but is too steep
at large r for Ellipticals (
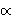 r-5).
r-5).
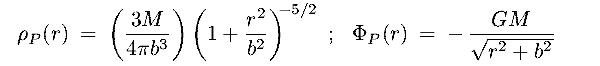 |
(8.7) |
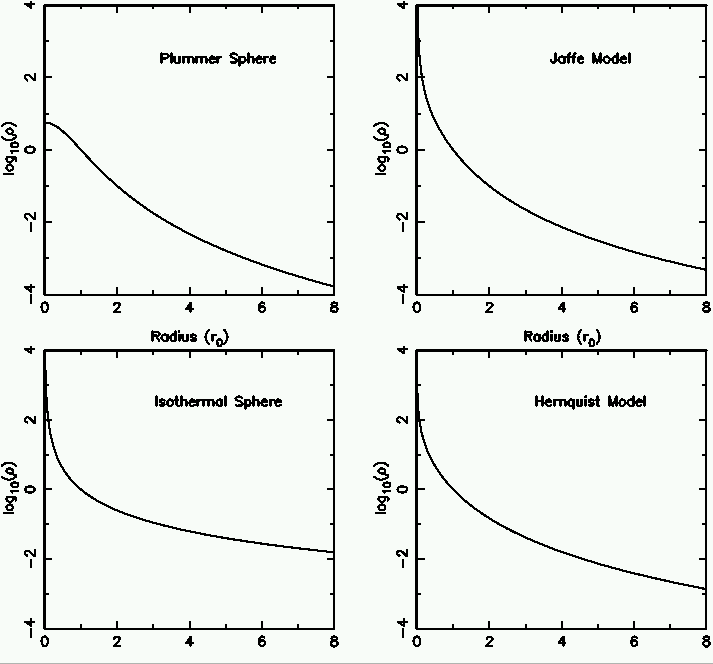
- Plummer; Isothermal; Jaffe; and Hernquist density laws are
shown here: [ image]
(vi) Axisymmetric Thin Disks
- Before considering global potentials for disks, first consider the vertical potential near z = 0
We have two conditions :
within a disk of volume density  o near
the plane
o near
the plane
above a disk of surface density 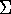
Using equation 8.3b we have :
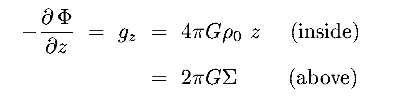 |
(8.8a) (8.8b) |
- Usually, calculating global
 and F for disks
is algebraically dense.
and F for disks
is algebraically dense.
Unlike spherical systems, disk potentials usually depend on mass outside R.
Here are two examples :
- Mestel's disk :
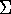 (R) =
(R) = 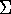 o Ro / R, has constant
Vc :
Vc2(R) = 2
o Ro / R, has constant
Vc :
Vc2(R) = 2 G
G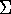 o Ro = GM(<R) / R
o Ro = GM(<R) / R
this is unusual in that Vc(R) doesn't depend
on mass outside R
- Exponential disk :
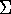 (R) =
(R) = 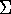 oexp(-R/Rd)
oexp(-R/Rd)
this fits the light profile of sprial disks much better than Mestel's disk, and has circular velocity
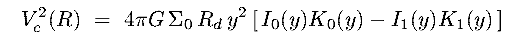 |
(8.9) |
where y = R / 2Rd, and In Kn are Bessel functions
or the 1st and 2nd kind
see [Topic 5.6a] for an analytic approximation and rotation curve.
(vii) Axisymmetric Flattened Systems
Spirals with bulge and disk are, of course, neither just spherical nor just thin disks
We need potentials which are both combined, ie flattened potentials
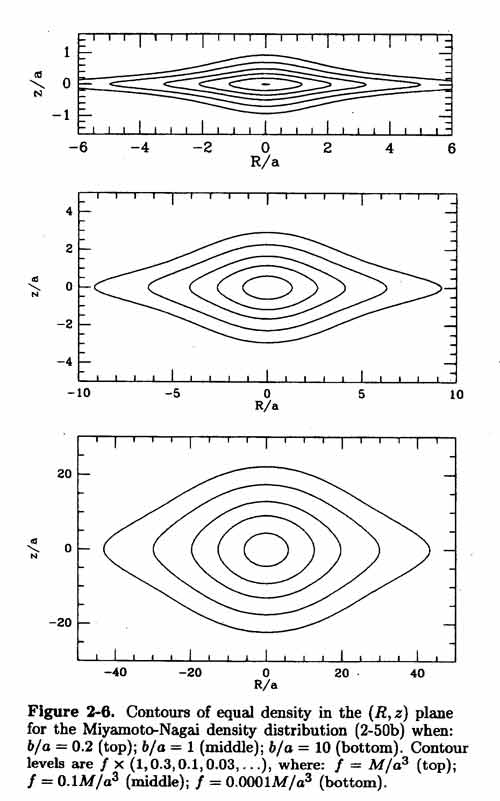
- Miyamoto-Nagai (1975) flattened system [ images ]:
reduces to the Plummer model if a=0 and the Kuzmin disk if b=0
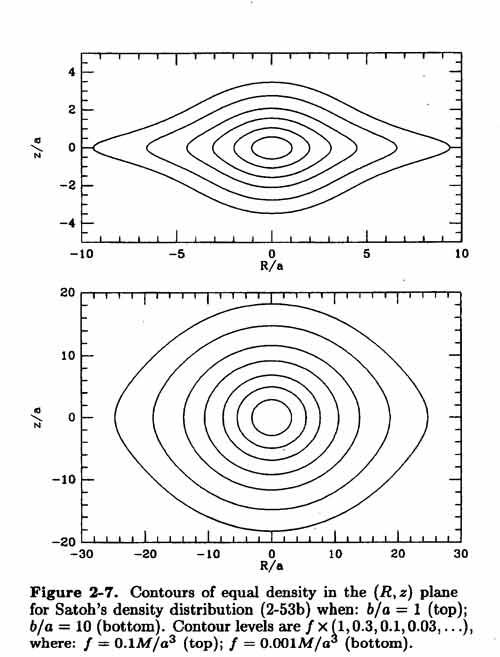
(Satoh flattened systems are derived in similar manner to the Toomre disks) [ images ] :
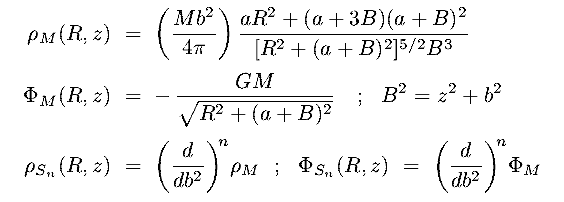 |
(8.11a) (8.11b) (8.11c) |
(viii) Triaxial Ellipsoids
- more complicated, (see B&T-2 § 2.5)
(ix) Multipole Expansion
An arbitrary mass distribution  sums of spherical
shells of non-uniform surface density.
sums of spherical
shells of non-uniform surface density.
Calculating the potential involves solving 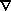 2
2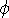 = 0 in spherical polar coordinates
= 0 in spherical polar coordinates
Solutions involve spherical harmonics : Yl,m
(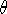 ,
,
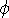 )
) 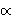 Pl|m|( cos
Pl|m|( cos 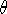 ) exp(i m
) exp(i m
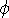 )
)
where Pl|m|(x) are associated Legendre functions.
The potential  (r,
(r,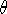 ,
,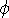 ) is the sum of a monopole (l=0), a dipole (l=2)
quadrupole (l=4) etc...
) is the sum of a monopole (l=0), a dipole (l=2)
quadrupole (l=4) etc...
each with associated amplitudes



(3) Orbit Classes
TBD



(4) Numerical N-Body Methods
Several methods are used :
See B&T-2 § 2.9 and
Josh Barnes's nice writeup for more details : (download .ps file here)



(5) The Virial Theorem
This fundamental result describes how the total energy (E) of a self-gravitating
system is
shared between kinetic energy (K) and potential energy (W)
Specifically, we are interested in their ratio :
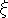 = K / |W| (note K is always +ve, W always -ve)
= K / |W| (note K is always +ve, W always -ve)
We begin by looking at two illustrative cases and then deal with the general case.
(a) Simple Illustrations
(i) Circular Orbit
-
Consider a satellite mass m in circular orbit about M (>>m) :
m V2 / r = G m M / r2
multiply by r :
m V2 = G m M / r  2K = -W or 2K + W = 0
2K = -W or 2K + W = 0

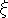 =
K / |W| = ½ and E = - K
=
K / |W| = ½ and E = - K
 Kinetic energy is half the (-ve) potential energy
Kinetic energy is half the (-ve) potential energy
 The total energy E = K + W is -ve and equal to (minus) the kinetic energy
The total energy E = K + W is -ve and equal to (minus) the kinetic energy
-
As we shall see,
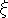 = ½ is a characteristic shared by a wide range of systems.
= ½ is a characteristic shared by a wide range of systems.
Note that in this case, the instantaneous values are also equal to the time averaged values
(ii) Time Averaged Keplerian Orbit
-
In general,
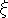 = K / |W| changes along a
Keplerian orbit path [image].
= K / |W| changes along a
Keplerian orbit path [image].
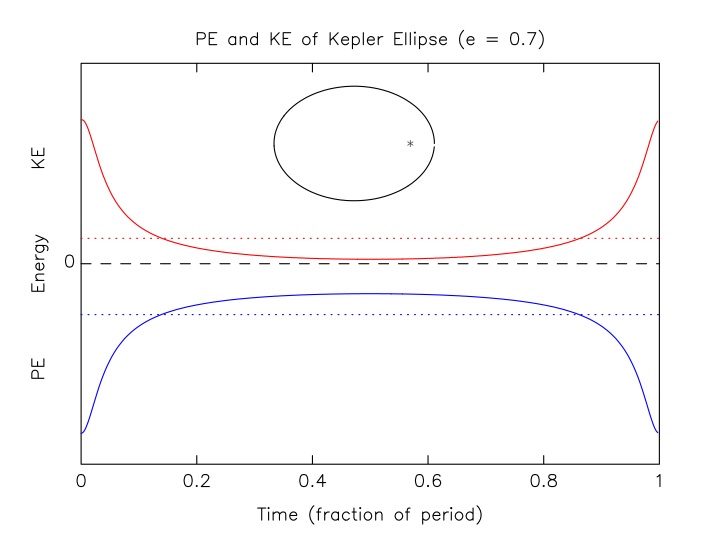
e.g. compare  at pericenter and apocenter :
at pericenter and apocenter :
 p /
p /
 a = ra / rp
a = ra / rp
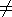 1 (using rp Vp = ra Va from AM conservation)
1 (using rp Vp = ra Va from AM conservation)
-
However, taking time averages over an orbit, we find :
< -W > = < GM/r > = GM < 1/r > = GM × (1/a), and
< K > = < ½ V2 > = GM < (1/r - 1/2a) > = ½GM × (1/a)
 and we recover, once again : <
and we recover, once again : <
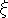 > = ½ and E = -< K >
> = ½ and E = -< K >
-
Note that time averages for single non-Keplerian orbits do not usually
have <
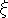 > = ½
> = ½
As we will see, however, 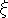 = ½ always holds
when we average over all particles in a system
= ½ always holds
when we average over all particles in a system
For our Keplerian orbit, m and M are the whole system
(with M having ~zero KE)
(b) The General Case
The general case comprises an isolated system of self-gravitating masses (see pdf)
Once again, we ask what is 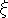 , the ratio of
kinetic to potential energies
, the ratio of
kinetic to potential energies
-
There are 3 equations of motion for member
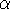 (i represents x, y, z) :
(i represents x, y, z) :
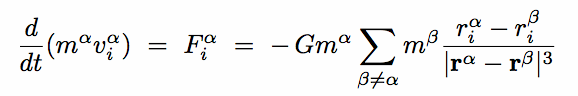 |
(8.12) |
- take the 1st moment in position : multiply by rj
 and sum over
and sum over
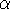 (j represents x,y,z)
(j represents x,y,z)
dimensionally, we have changed an equation of forces into an
equation of energies
after some algebra, we get a set of 9 equations
these can be neatly written using 3 × 3 matrices (i.e. tensors of order 2)
this set of equations constitute the Tensor Virial Theorem :
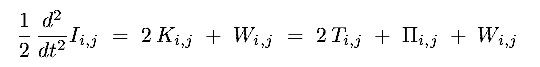 |
(8.13) |
where the five tensors are :
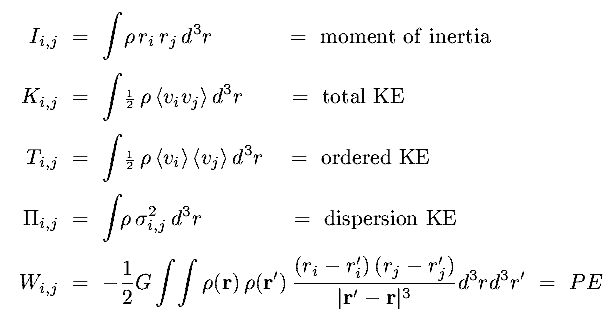 |
(8.14)
(a,b,c,d,e) |
where  i,j arises from the expansion: <vi vj> = <vi><vj> +
i,j arises from the expansion: <vi vj> = <vi><vj> +  i,j2
i,j2
- For steady state systems, d2Iij / d t2 = 0
and we get
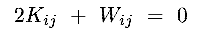 |
(8.15a) |
the Kinetic and potential energies are related for each tensor element
for example, they are related separately along each axis
- Considering just the diagonal terms, we also have :
Trace(T) + ½ Trace(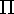 )
)  K = total kinetic energy, and
K = total kinetic energy, and
Trace(W)  W = total potential energy
W = total potential energy
so for the static case, we get the Scalar Virial Theorem :
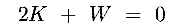 |
(8.15b) |
- Considering the total energy, E, we find :
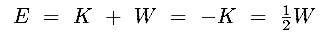 |
(8.15c) |
So the total energy is negative : the system is bound !
its value is equal to either
minus the (+ve) Kinetic Energy, or
half the (-ve) Potential Energy
- Here is a very useful little diagram to illustrate the situation :
[image]
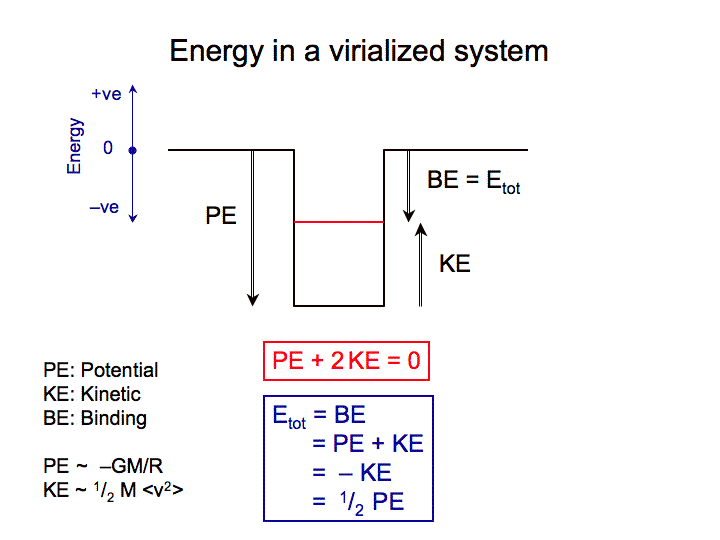
- Briefly reviewing the conditions necessary to use these simple equations :
the system must be self gravitating
the system must be in steady state (orbit timescale << evolution timescale)
quantities must be time averaged (or many objects sampled with random
orbital phase)
the system must be isolated (or at least embedded in a slowly varying
potential)
Note that the system may be either collisionless (stellar) or collisional (gaseous)
(c) Mass Determination
- The most famous use of the virial theorem is to determine the masses
of stellar systems.
For a system of total mass M and mean squared velocity <v2>,
K is simply ½ M <v2>
The virial theorem then gives :
<v2> = -W / M  GM / Rg
GM / Rg
which in practice defines the gravitational radius: Rg
Knowing Rg and measuring <v2> allows us to
determine M, the system mass.
What to use for Rg isn't obvious for most stellar systems
with no clear "edge" or "size"
However, we can make use of the median radius : Rm which
encloses half the mass
For many stellar systems, it turns out that Rg 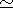 Rm / 0.4
(note Rm is written rh in B&T)
Rm / 0.4
(note Rm is written rh in B&T)
We then have :
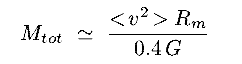 |
(8.16) |
which resembles the circular orbit relation: M = V2 R / G, but applies to a general self-gravitating system.
(d) Binding Energy : Energy Released During Collapse
(e) Stellar Systems Have Negative Specific Heat
(f) Rotational Flattening
- Consider an axisymmetric system rotating about the z axis
By symmetry :
T, 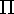 , and W are all diagonal
, and W are all diagonal
x & y elements of these tensors are the same
- The tensor virial theorem gives :
2 Txx + 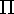 xx
+ Wxx = 0
xx
+ Wxx = 0
2 Tzz + 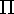 zz
+ Wzz = 0
zz
+ Wzz = 0
- We also have :
Tzz = 0 (rotation about z
 no drift
no drift
 to z)
to z)
2 Txx = ½ 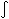
 <V
<V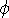 >2
d3r = ½ M Vo2
(Vo is the mass weighted rotation speed)
>2
d3r = ½ M Vo2
(Vo is the mass weighted rotation speed)
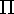 xx = M
xx = M
 o2
(
o2
(  o is the mass weighted dispersion)
o is the mass weighted dispersion)
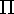 zz
zz  (1 -
(1 - 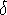 )
) 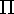 xx
= (1 -
xx
= (1 - 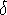 ) M
) M
 o2 (
o2 ( 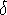 < 1, measures anisotropy)
< 1, measures anisotropy)
Wxx / Wzz 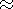 (A/B)0.9 = (1 -
(A/B)0.9 = (1 -  )
-0.9 (A/B is axis ratio of isodensity surfaces)
)
-0.9 (A/B is axis ratio of isodensity surfaces)
- Finally, substituting all these into the ratio of the two tensor relations
above, we get :
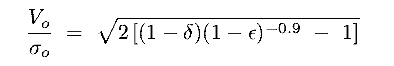 |
(8.17a) |
B&T-1 fig 4.5 shows this relation for several 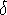 ,
including projection corrections [image]
,
including projection corrections [image]
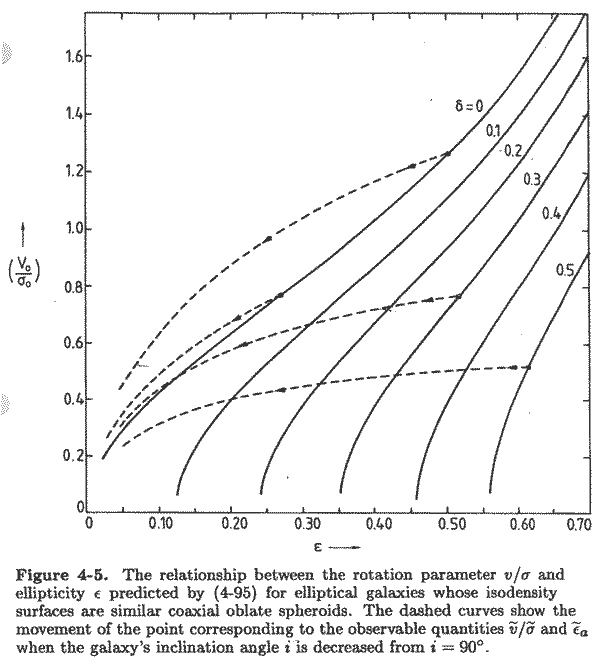
For isotropic velocities, 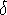 = 0,
and we get, for small
= 0,
and we get, for small  :
:
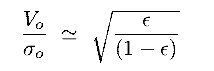 |
(8.17b) |
- In this case, the inclination
corrections to Vo /
 o
and
o
and  are similar, so the prediction is robust
are similar, so the prediction is robust
- Observationally, in Topic 7 we found (B&T-1 fig 4.6;
[images]
 Low luminosity Ellipticals and Bulges follow the isotropic relation
Low luminosity Ellipticals and Bulges follow the isotropic relation
 Luminous Ellipticals often fall in the anisotropic
(
Luminous Ellipticals often fall in the anisotropic
(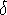 > 0) region
> 0) region



(6) Describing Collisionless Systems
We first consider collisionless dynamics :
- "Collision", here, means star-star deflection, not direct impact
For the collisionless case, stars are assumed to move in a completely smooth potential
(in § 8.10 we consider when and how star-star encounters are relevant).
Let's briefly justify why this is the case.
- Consider the chances of actual star-star collisions in the solar neighborhood:
A typical star size/separation is: size ~D(sun) ~1/100 AU (sun ½ deg); sep ~1pc ~105AU
 Size/sep ~10-7
Size/sep ~10-7
 filling factor ~10-21
(note, for air : 10-1.5 & 10-4.5)
filling factor ~10-21
(note, for air : 10-1.5 & 10-4.5)
Illustration: star = fine grain of sand (~0.1mm)  typical galaxy ~1011 = cubic yard of sand
typical galaxy ~1011 = cubic yard of sand
But, each separated by ~1km (10m in nucleus)  fills Earth
fills Earth  very empty.
very empty.
[Note: since dynamical time t ~ 1 / (G  )½ &
)½ &  sand ~
sand ~  star, then
star, then
the sparse sand model & MW galaxy have the same gravitational timescale: ~100 Myr ].
- Path length: 1/n
 = sep3/size2 = (sep/size)2 x sep = 1014pc ~109 orbits!
= sep3/size2 = (sep/size)2 x sep = 1014pc ~109 orbits!
 Collision time: ~1017yrs @ 200 km/s (~1018yrs @ disk dispersion).
Collision time: ~1017yrs @ 200 km/s (~1018yrs @ disk dispersion).
Hence the famous statement: when two galaxies collide, no stars collide.
Alternate perspective: typical star-star encounter deflection ~½ arcsec
Hence, star orbits follow smooth potential.
[movie].
- Notice that Dark Matter (elementary particles) also behaves in a collisionless manner.
Strange: usually view particles as bouncing around, but these move on smooth orbits
 to first order, DM particles and stars share similar dynamics.
to first order, DM particles and stars share similar dynamics.
However, DM currently more extended, so how did this arise?
 gas behaves differently
gas behaves differently
 settles before forming stars.
settles before forming stars.
(a) The Distribution Function (DF) : f(r, v, t)
(b) Collisionless Boltzmann (Vlasov) Equation (CBE)
- Look for a continuity equation, since :
no stars created/destroyed : flow conserves stars
stars do not jump across the phase space (ie no deflective encounters)
View the DF as a moving fluid of stars in 6-D space (r, v), ie x,y,z,vx,vy,vz
stars move/flow through the region as their positions and velocities change
- Consider a 1-D example using x and vx, and recall f is a number
density
focus on a small element of phase space at x and vx with size
dx by dvx
this [image] will help visualize the situation
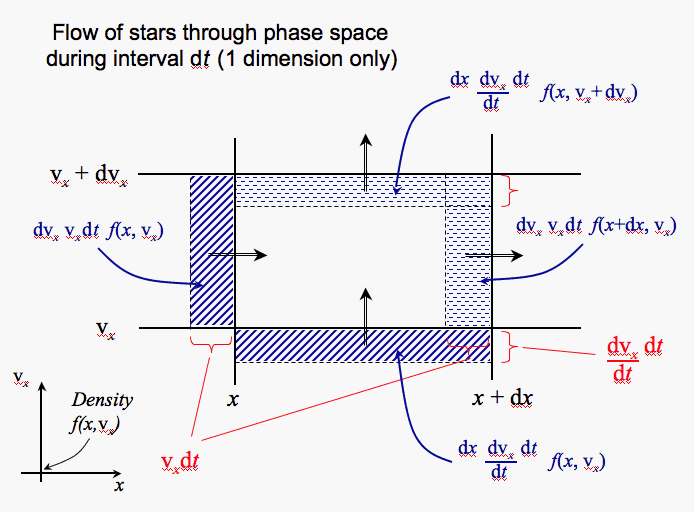
- In interval dt, net flow in x is :
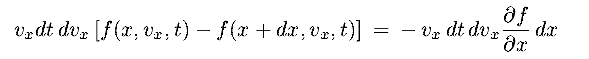 |
(8.18a) |
the net flow due to the velocity gradient is
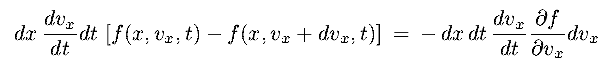 |
(8.18b) |
the sum of these equals the net change to f in the region, ie at x, vx of size dx dvx
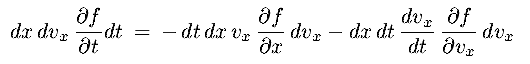 |
(8.18c) |
or, dividing by dx dvx dt, we get
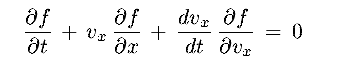 |
(8.19a) |
but since
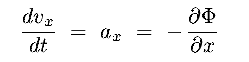 |
(8.19b) |
we have
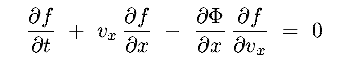 |
(8.19c) |
adding the y and z dimensions, which are independent, we finally have
This is the collisionless Boltzmann equation (CBE)
-
The CBE describes how the DF changes in time
It is a direct consequence of :
| 1 conservation of stars |
| 2 stars follow smooth orbits |
| 3 flow of stars through r defines implicily the location v (= dr/dt) |
4 flow of stars through v is given explicitly by -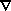  |
|
- Since
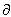 f/
f/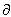 t
is a Eulerian (partial) differential, it describes the change in
DF at a point in phase space
t
is a Eulerian (partial) differential, it describes the change in
DF at a point in phase space
- However, consider the Lagrangian (total, or convective)
derivative : Df/Dt
 df/dt.
df/dt.
This describes the change in f as we follow along the "orbit" through phase space
But, this Lagrangian derivative is nothing more than the LHS of the CBE
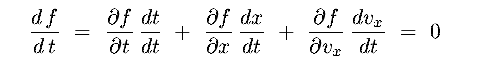 |
(8.20) |
Clearly, the phase space density (f) along the star's orbit is constant
ie the flow is "incompressible" in phase-space
for example
if a region gets more dense,  will increase
will increase
if a region expands,  will decrease
will decrease
example -- marathon race : start : n high, 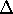 v high ;
end : n low,
v high ;
end : n low, 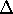 v low
v low
- The CBE applies to all sub-populations of stars (eg each
spectral class)
even though no single class determines the potential
in § 8.7b we introduce a self-consistent f which itself generates
 :
:
(c) The Jeans Equation(s)
- As it stands, the CBE is of rather limited use :
- the constraints it provides are still insufficient to find
f(r,v,t)
- the complexity of f(r,v,t) renders it observationally inaccessible.
- What we observe are :
- mean velocities : < v >
- velocity dispersions :
 (which is related to < v2 > )
(which is related to < v2 > )
- stellar densities : n (also
 for mass density, or j for luminosity denisty)
for mass density, or j for luminosity denisty)
We need to recast the CBE in terms of these quantities.
-
Clearly, these observable quantities are contained within the DF :
f (r,v,t)
they can be extracted by taking appropriate averages or
moments
for example :
number density = n(r, t) =
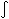 f(r, v, t) d3v
= 0th moment in v
f(r, v, t) d3v
= 0th moment in v
mean velocity = <vi(r, t)> =
(1/n)
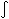 vi f(r, v, t)
d3v = 1st moment in v
vi f(r, v, t)
d3v = 1st moment in v
If we take moments of the CBE, we transform it into equations in these
new variables.
Lets look in more detail at these first two moments in v (see B&T-2 §4.8) :
- Using the 1-D x axis as example, simply integrate the CBE (eq 8.19c)
over all vx
We obtain (0th moment in vx) :
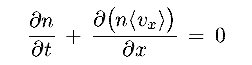 |
(8.21) |
where n  n(x,t) is the space density and
<vx> is the mean drift velocity along x
n(x,t) is the space density and
<vx> is the mean drift velocity along x
This is a simple continuity equation for the number of stars along the
x axis.
- Now multiply the CBE (eq 8.19c again) through by vx and
again integrate over all vx
on rearranging and using eq 8.21 above, we obtain (1st moment in vx) :
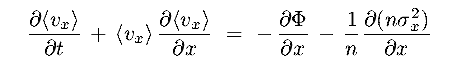 |
(8.22a) |
where
 x2 is the velocity
dispersion about the mean velocity,
x2 is the velocity
dispersion about the mean velocity,
it arises from <vx2>
= <vx>2 +  x2
x2
- repeating this in 3-D requires a little care (B&T-2 § 4.8) :
we obtain the Jeans Equation (for coordinate j) :
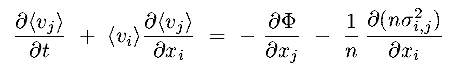 |
(8.22b) |
where the summation convention applies (sum over repeated indices)
here, i=1,2,3 and j=1,2,3 refer to x,y,z, eg x2
 y and v2
y and v2
 vy
vy
-
This Jeans equation is akin to Newtons's second law : dv/dt = F/m with :
LHS is the derivative of <v>
RHS are force terms
- It is instructive to compare this to
Euler's Equation for fluid flow :
 |
(8.23) |
which is clearly analogous.
-
In 8.22b n
 i,j2 is a
stress tensor which takes the role of an anisotropic pressure
i,j2 is a
stress tensor which takes the role of an anisotropic pressure
(hence the phrase "pressure supported")
in a fluid, pressure is a scalar and is therefore always isotropic
for stellar systems,  i,j is a
tensor which can be anisotropic
i,j is a
tensor which can be anisotropic
-
 i,j is symmetric, : i.e. axes exist where
i,j is symmetric, : i.e. axes exist where  1,1,
1,1,
 2,2,
2,2,  3,3 are semi-axes of a velocity ellipsoid
3,3 are semi-axes of a velocity ellipsoid
if  1,1 =
1,1 =
 2,2 =
2,2 =  3,3 we have isotropic dispersion
3,3 we have isotropic dispersion
 Jeans and Euler equations are identical
Jeans and Euler equations are identical
-
For collisionless systems there is
no equation of state linking pressure (
 i,j2) to density
i,j2) to density
Usually, therefore, we are forced to assume  i,j (or, equivalently, the anisotropy
parameter
i,j (or, equivalently, the anisotropy
parameter 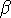 )
)
Recently, however, the LOSVD has been used
to constrain 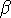 (see T 5.7a :
[link]).
(see T 5.7a :
[link]).
(d) Applications of the Jeans Equation
The Jeans equation, when combined with
observations, has a number of applications :
-- deriving M/L profiles in spherical galaxies (B&T-1 4.2.1d)
-- deriving the flattening of a rotating spheroid with isotropic velocity
dispersion (B&T-1 4.2.1e)
-- analysis of asymmetric drift (B&T-1 4.2.1a)
-- surface density (and volume density) in the galactic disk (B&T-1 4.2.1b)
-- analysis of the local velocity ellipsoid in terms of Oort's constants (B&T-1 4.2.1c)
Here we look briefly at the first and second :
(i) Spherically Symmetric Steady State Systems
-
This is, of course, an important special case to consider :
For steady state, the first term in Eq 8.22b is zero
For spherical symmetry : <vr> = <v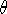 > = 0,
giving < vr2 > =
> = 0,
giving < vr2 > =  r2 and
< v
r2 and
< v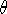 2 > =
2 > = 
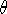 2.
2.
After transforming to spherical polar coordinates, the Jeans Equation reads
:
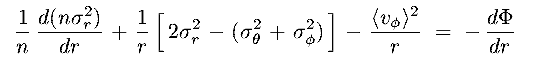 |
(8.24a) |
Introducing anisotropy parameters :
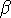
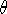 =
1 -
=
1 - 
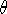 2 /
2 /  r2
and
r2
and 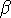
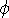 =
1 -
=
1 - 
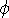 2 /
2 /  r2
r2
and writing 2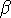 for
for 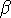
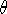 +
+ 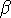
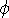 and Vrot for
<v
and Vrot for
<v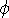 > this becomes
> this becomes
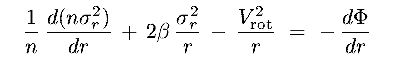 |
(8.24b) |
which is equivalent to the equation of hydrostatic support :
dp /dr + anisotropic correction + centrifugal correction = Fgrav
-
Going a little further, recasting
d
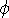 / dr as
GM(<r) / r2 = Vc2 / r
(Vc = circular velocity)
/ dr as
GM(<r) / r2 = Vc2 / r
(Vc = circular velocity)
and rewriting the first term in eq 8.24b in logarithmic gradients,
we have :
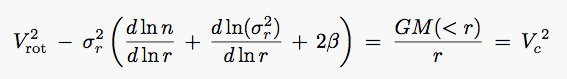 |
(8.24c) |
This parallels the equation for hydrostatic support of an ideal gas, where
p = nkT
the equivalences are :
 r2
r2  T
T
d(ln n) / d(ln r) + d(ln T) / d(ln r)
 (n/p) dp / dr
(n/p) dp / dr
2 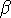 and Vrot2
are anisotropy and rotation correction terms
and Vrot2
are anisotropy and rotation correction terms
-
By measuring brightness profiles and velocity dispersion & rotation profiles,
we can derive (assuming 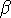 ) : M(r) and hence
M/L (r)
) : M(r) and hence
M/L (r)
This is very important, eg, in the search for nuclear black holes (see Topic 14.2 :
link)
(ii) Rotational Flattening Revisited.
TBD
(iii) Vertical Disk Structure.
TBD



(7) Steady State : The DF as f(E, |L|, Lz)
Taking moments of the CBE lost almost all detailed information from the
DF
Rather than working with the full DF, the Jeans equation works with just n, <v> and <v2>
Can we reintroduce the full DF and regain a more complete description of
a system ?
The answer is yes, by introducing two new powerful constraints :
 demand that the system is in steady
state (
demand that the system is in steady
state ( in equilibrium)
in equilibrium)
 demand that the DF generate the
full potential (not just act as a tracer population)
demand that the DF generate the
full potential (not just act as a tracer population)
We consider these in turn
(a) Integrals of Motion and the Jeans Theorem
- When a system is in steady state,
 and f are not explicit functions of time
and f are not explicit functions of time
In this case, we may introduce a powerful new
entity : Integrals of motion
An "integral of motion" is a function I (r, v) which
is constant along a star's orbit (B&T-1 § 3.1.1)
Obvious examples of possible integrals of motion are :
| E (r, v) | = ½v2 +  (r) (r) | = energy per unit mass |
in a static potential |
|
L (r, v) | = r × v | = total AM | in a spherical static potential |
|
Lz (r, v) | = (x2 + y2)½ v
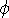 | = z component of AM | in an axisymmetric static potential
| |
- Since I (r, v) is constant along an orbit, it is also
a solution to the steady state CBE
specifically :
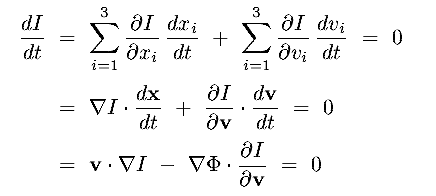 |
(8.25) |
- Since the CBE is a linear equation, then functions of solutions are
themselves solutions
This yields the Jeans Theorem :
|
Any function of integrals of motion f (I1, I2, I3, ..... ) is also a solution of the steady state CBE
|
- This is extremely useful since it allows us to construct
legitimate DFs using integrals of motion :
eg,: the DF : f (E, Lz) = No (E2 +
3Lz5/2) is a solution to the CBE for an
axisymmetric potential
- In the special case of steady state spherical systems,
it is easy to show (B&T-1 § 4.4.2) that :
-
DFs must have the form f(E, |L|)
-
DFs of the form f(E) must have an isotropic velocity dispersion
 r =
r =

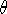 =
=

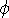
-
DFs of the form f(E, |L|) must have an anisotropic velocity dispersion
 r
r 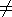

 =
=

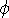
- Summarizing: these theorems provide a very useful way to begin constructing working models :
For each r and v location in phase space calculate, for example, E, |L|, Lz
Now assign the number of stars at that location in phase space, f(r,v), by some function of E, |L|, Lz.
These DFs now automatically satisfy the continuity condition expressed
by the steady state CBE.
(b) Self-Consistency
- Both the CBE and the Jeans Equation include a potential gradient,

In neither equation, however, are these potentials linked explicitly to the
DF
(recall  f(r, v) d3v =
n(r)
f(r, v) d3v =
n(r)

 (r) which
could, in principle, define
(r) which
could, in principle, define  )
)
As it stands, the DFs only describe tracer populations.
- Clearly, an important step is to require that the DF also
yields the potential
 (r)
(r)
ie :
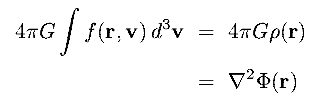 |
(8.26a) (8.26b) |
where f here is the mass DF (ie we've multiplied f by the mean stellar mass)
- Taking the spherical form for
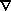 2, this reads (eg for a DF of the form f (E, |L|) :
2, this reads (eg for a DF of the form f (E, |L|) :
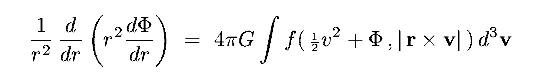 |
(8.27) |
This is now a fundamental equation describing spherical equilibrium systems.
Solutions not only have self consistent  and f, but
f also satisfies the steady state CBE.
and f, but
f also satisfies the steady state CBE.
Such a solution now describes a self-consistent, physically plausible stellar
dynamical system.
- When using this equation to solve the structures of many systems,
we introduce (B&T-1 § 4.4) :
-
relative potential :
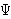 =
=  o -
o - 
-
relative energy : Er = -E +
 o =
o = 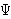 - ½ v2
- ½ v2
-
note : both
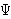 and Er are more +ve
for more bound stars deeper in the system
and Er are more +ve
for more bound stars deeper in the system
-
choose
 o so that f > 0 for Er > 0 (bound)
o so that f > 0 for Er > 0 (bound)
-
at given
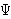 : Er spans range 0 to
: Er spans range 0 to 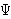 , as v spans the range from
, as v spans the range from 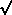 (2
(2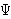 )
( = Vesc) to 0
)
( = Vesc) to 0
(c) Spherical Isotropic Systems : DF = f(Er)
(d) Deriving f(Er) from  (r) for
Non-Rotating Spherical Systems
(r) for
Non-Rotating Spherical Systems
(e) From f(Er)d3r d3v to N(Er)dE



(8) Model Building Using DFs
We begin with the simplest cases : equilibrium, non-rotating, spherical systems,
ie DF  f(Er)
f(Er)
With equations 8.28a,b now in hand, we are ready to construct specific models
The process goes as follows :
(1) Choose a DF which is a function of energy : f(Er)  f(
f(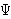 - ½v2)
- ½v2)
from Jeans Theorem, f(Er) is already a solution to the steady state CBE,
so our solutions will naturally satisfy the basic phase space continuity condition
(2) Integrate the DF over v to find  (
(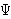 ) (ie evaluate 8.26a)
) (ie evaluate 8.26a)
(3) Solve Poisson's equation (8.28a) to find 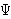 (r)
(r)
(4) Combine  (
(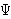 )
and
)
and 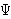 (r)
to give the mass distribution :
(r)
to give the mass distribution :  (r)
(r)
Here are some examples
(a) Polytropic Sphere: Power Law f(Er)
- Consider a power law DF : f(Er) = F Ern-(3/2)
for Er > 0 (otherwise f(Er) = 0)
Integrate f(Er) over velocity to find the density in terms
of 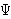 (eq 8.26a) :
(eq 8.26a) :
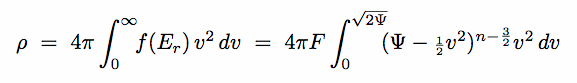 |
(8.31) |
after substituing v = (2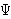 )½cos
)½cos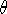 ,
we find
,
we find  (
(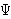 ) = cn
) = cn
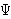 n (
n (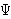 > 0)
> 0)
where cn is a constant depending on n and F.
- Substitute this into the spherical version of Poisson's equation (eqn 8.28a) :
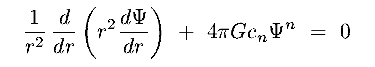 |
(8.32) |
- This is the Lane-Emden equation, first studied as the equation describing hydrostatic
equilibrium of a self-gravitating sphere of polytropic gas
(ie equation of state : p 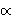

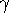 )
)
Thus, we find that for a self-gravitating sphere, the density profile  (r) is the same for
(r) is the same for
Stars with DF  Ern-(3/2), and
Ern-(3/2), and
Gas with polytropic equation of state and  = 1 + (1/n)
= 1 + (1/n)
- Simple solutions only exist for n = 5 (
 = 6/5)
= 6/5)
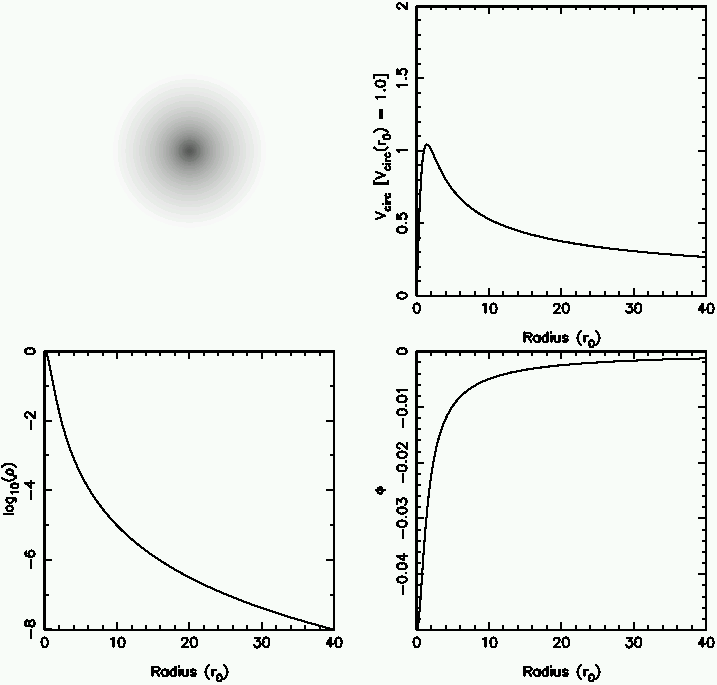 This is the Plummer Sphere with
This is the Plummer Sphere with
 (r)
(r) 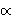 (1 + (r/b)2)-5/2
(1 + (r/b)2)-5/2
It has finite mass and is well behaved at r = 0
It is a good match to Globular Clusters but is too steep at large r for Ellipticals
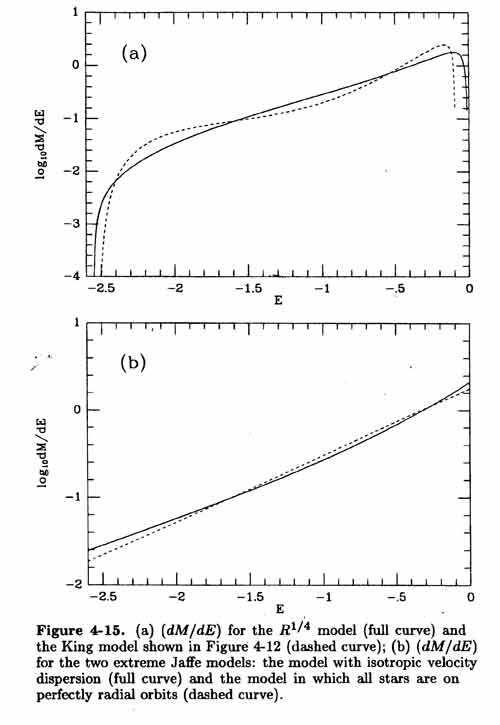
Density; potential; rotation &
image for a Plummer sphere are shown here : [image]
- n > 5 systems are more extended and have infinite mass
Density profiles for n=0,1,2,3,4,5 are shown here : [image]
- n =
 so
so  = 1 and p
= 1 and p 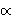
 which is
the isothermal equation of state (recall P = n k T )
which is
the isothermal equation of state (recall P = n k T )
for n = 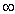 the above analysis breaks down, but we have an alternative approach :
the above analysis breaks down, but we have an alternative approach :
(b) Isothermal Sphere: Exponential f(Er)
- Consider an exponential (Boltzmann) DF
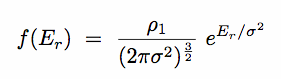 |
(8.33) |
Recall, more +ve  & Er means more bound.
& Er means more bound.
Also, note f(Er) > 0 for Er < 0: there are unbound stars! .... we anticipate problems at large radii.
OK, substituting  - ½v2 for Er and integrating f(Er) over v gives
- ½v2 for Er and integrating f(Er) over v gives
 =
=  1 exp
(
1 exp
( /
/  2)
2)
-
Plugging this into Poisson's equation gives :
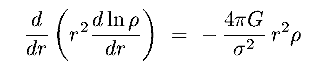 |
(8.34) |
This is, in fact, the equation for a hydrostatic
sphere of isothermal gas, with  2 =
kT/m
2 =
kT/m
Why is this ?
At every point, N(v)  exp(-½v2/
exp(-½v2/ 2), for both
the stellar system and a gas of atoms
2), for both
the stellar system and a gas of atoms
it is irrelevant, therefore, whether the stars are collisionless or not, they
mimic a gas of atoms.
-
Traditionally, we consider the solutions to 8.34 as (i) "a special case" and
(ii) "the rest" :
(i) Singular Isothermal Sphere (SIS)
-
For the central boundary condition
 (0) =
(0) =
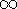 we have
we have
 (r) =
(r) =  2 / (2
2 / (2 G r2)
G r2)
this is the singular isothermal sphere:

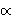 r-2
r-2
-
Circular velocity : Vc = const =

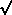 2
2
-
Dispersion velocity :
<v2> = 3
 2
everywhere (isothermal !); 1-D : <vr2> =
2
everywhere (isothermal !); 1-D : <vr2> =  2
2
-
But the model has infinite density at r = 0, and has infinite mass
as r

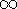 !
!
-
Density; potential; rotation &
image for SIS are shown here : [image]
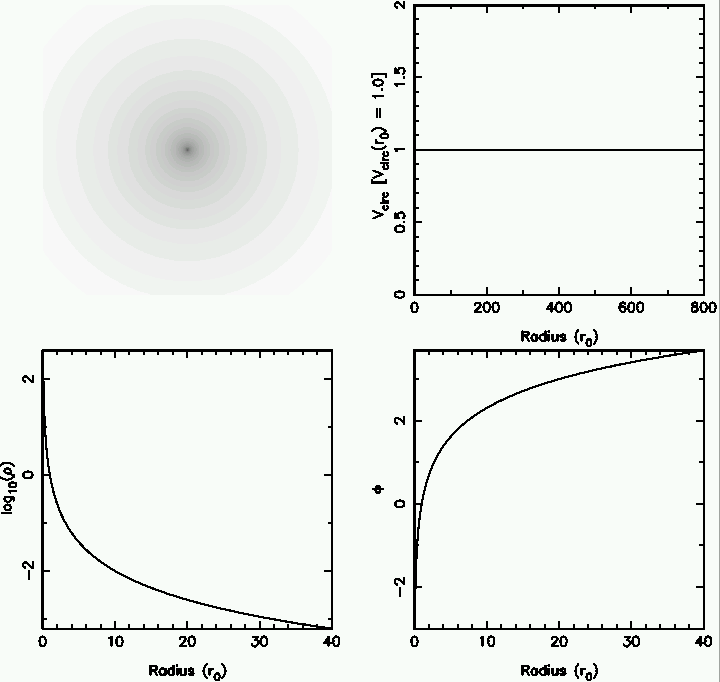
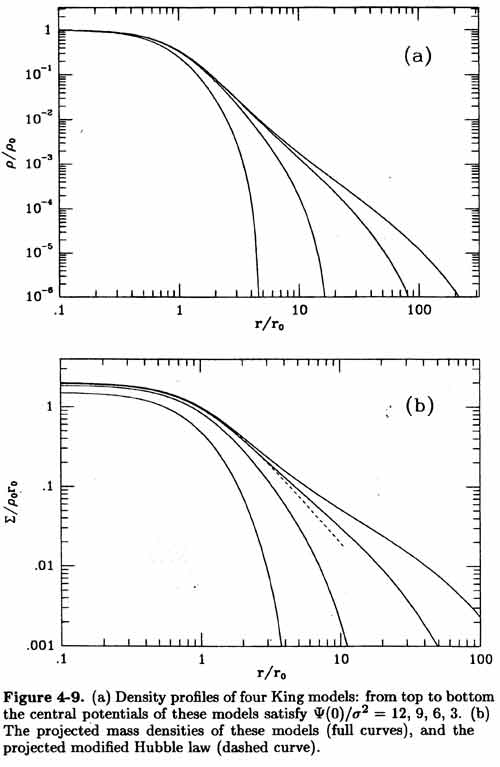
(ii) General Isothermal Sphere
- Choose as central boundary conditions at r = 0 :
 (0) =
(0) =  o
finite central density
o
finite central density
(d /dr )r=0 = 0 flat central density
profile
/dr )r=0 = 0 flat central density
profile
Integration of 8.34 with these boundary conditions yields  (r)
[image]: B&T-1 figs 4.7, 4.8
(r)
[image]: B&T-1 figs 4.7, 4.8
-
We find a constant near-nuclear density :
 (r) ~
(r) ~  o within a radius ro =
3
o within a radius ro =
3  / (4
/ (4 G
G  o)½
o)½
This is a core and ro is called the King (or core) radius
I(ro) = 0.5013 I(0), so ro is appropriately defined
ro is also the scale length of the
r-2 envelope (see below): big cores are in big galaxies
Circular velocity : Vc = - (d ln
(d ln  / d ln r)½
/ d ln r)½
-
When plotted as log (
 /
/  o) vs log (r / ro), there is only
one isothermal profile
o) vs log (r / ro), there is only
one isothermal profile
-
The scale length and central density together
define the dispersion :
 2
2 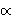
 o
ro2
o
ro2
 for a given central density, hotter galaxies are larger
for a given central density, hotter galaxies are larger
 for a given core radius, hotter galaxies are denser
for a given core radius, hotter galaxies are denser
-
Quantitatively :
 2 = (4 / 9)
2 = (4 / 9)  G
G  o
ro2
o
ro2
To simplify calculations, use G = 4.5 × 10-3 in units of pc, km/s, and M
Eg for  = 100 km/s, ro = 100 pc we have
= 100 km/s, ro = 100 pc we have
 o = 159 M
o = 159 M pc-3
pc-3
-
A good isothermal core match to the centers of Ellipticals can be used
to estimate central M/L
 obtain ro and I(0) from isothermal fits to I(R), and measure
obtain ro and I(0) from isothermal fits to I(R), and measure 
(express I(0) in units of L  pc-2 to allow simplified calculations with G = 4.5 × 10-3)
pc-2 to allow simplified calculations with G = 4.5 × 10-3)
j(0) = 0.5 I(0) / ro
 (0) = 9
(0) = 9  2/
(4
2/
(4 G ro2)
G ro2)
M/L =  (0) / j(0)
(0) / j(0)
This method is called "core fitting" or "King's method"
Typical values for ellipticals cores are  10-20 h M
10-20 h M / L
/ L suggesting minimal/no dark matter
suggesting minimal/no dark matter
-
There is a problem with all isothermal models: they have infinite total mass
It is easy to see why the system is at least infinite in extent :
at any given radius, stars have isotropic dispersion 
at this radius at least some stars are therefore moving outward
but further out the dispersion is still  ,
and stars are moving outward
,
and stars are moving outward
 the system must have infinite extent
the system must have infinite extent
Ultimately, this arises because f(Er) > 0 for negative Er, i.e. the model includes unbound stars.
To rectify this problem, we attempt to modify things slightly by removing the unbound stars: 
(c) Lowered Isothermal (King): Truncated Exponential f(Er)
(d) Other Models
The methods illustrated here can be applied to more complex systems:
Spherical systems with velocity anisotropy (B&T-2 4.3.2)
Axisymmetric systems (B&T-2 4.4)
Thin disks (B&T-2 4.5)



(9) Violent Relaxation
-
The previous discussion focussed on static systems, since
they are relatively tractable.
Varying potentials are usually intractable and
require a numerical approach.
There are, however, a few situations which can be treated analytically
Paradoxically, one of these is when the potential is maximally fluctuating
This is the case of violent relaxation, which we now describe briefly
-
For galaxies, 2-body encounters are negligible and evolution is
determined by the CBE
For a static potential, energy (E) of a star is conserved and the
DF doesn't change
Isolated galaxies in steady state do not, therefore, evolve dynamically
(we're ignoring gas & 2-body processes here)
- For a galaxy to change, there needs to be a changing potential
For each star, dE / dt = 
 /
/  t at the star
t at the star
The DF evolves and the structure of the galaxy changes
This occurs during (i) inhomogeneous collapse, and (ii)
encounters (Topic 12)
These are brief traumatic times :
 "galaxy changes are by revolution rather than by evolution"
"galaxy changes are by revolution rather than by evolution"
(nice quote from Binney's EAA article)
-
In collapse of large cold system,
 changes
rapidly
changes
rapidly

Stars gain and lose energy, which broadens f(E)
Energy is redistributed via collective interactions
This acts like a relaxation process [image & movie].
-
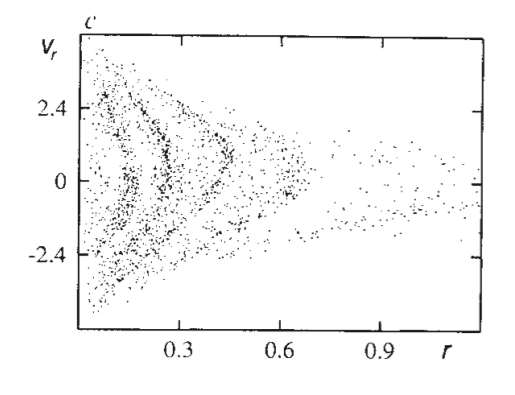
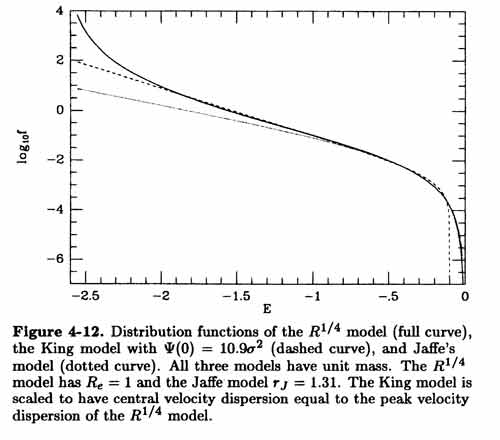
N-Body example: van Albada 1982 (B&T 4.7.3)
([images] : B&T figs 4.19-22)
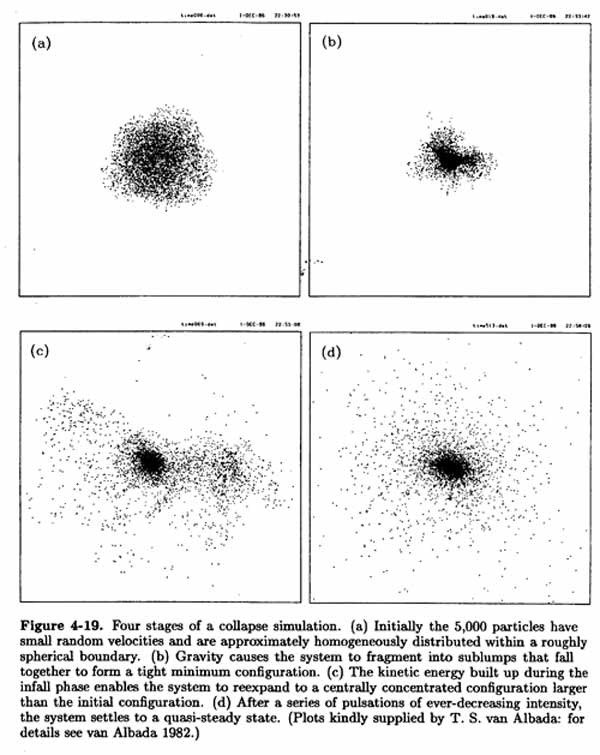 Start with ~ homogeneous sphere with low
Start with ~ homogeneous sphere with low  (Similar to Klypin simulation above).
(Similar to Klypin simulation above).
1st infall: clumps grow; infall speeds up; dense inhomogeneous center; much scattering
Rebound: stars fly back out; some lost; many stay near center
Oscillations die down; system settles into ~ R¼ law; with
 decreases outwards
decreases outwards
Anisotropy, 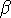 , is 0 at nucleus,
, is 0 at nucleus,  1 at edge
1 at edge
(Most scattering occurs at small r on 1st infall  most stars have low AM
most stars have low AM
N(E) dE spreads out, most stars have E ~ 0, few are deeply bound
-
Note: the total energy remains constant : this is a
non-dissipational process
energy is not radiated away, as with dissipational (gaseous) collapse
If the total energy is initially zero (eg diffuse system at rest), then
following collapse :
some stars will be strongly bound, but some must also have been ejected.
-
Note: scattering is independent of the star's mass
fundamentally different from 2-body relaxation
no segregation by mass (eg heavy stars don't sink to center)
-
Phase mixing helps smooth out lumps fairly quickly
distribution is ~smooth after ~few collapse times
 violent relaxation timescale is
~few × dynamical (collapse) timescale
violent relaxation timescale is
~few × dynamical (collapse) timescale
-
If relaxation is complete, then fully random scattering occurs
 results in isotropic velocity field and Boltzmann-like f(E)
results in isotropic velocity field and Boltzmann-like f(E)
Usually, however, the density distribution becomes smooth before
scattering is complete.
Relaxation ceases and is incomplete
 residual anisotropies & phase-space substructures
[images & movie]
residual anisotropies & phase-space substructures
[images & movie]
-
If the initial distribution is hotter
 less concentrated
less concentrated
If the initial distribution is rotating slowly  less concentrated & rotating oblate figure
less concentrated & rotating oblate figure
If the initial distribution is rotating faster  even less concentrated & prolate/bar figure
even less concentrated & prolate/bar figure
If the initial distribution is ellipsoidal  rotating ellipsoid, anisotropic everywhere [image]
rotating ellipsoid, anisotropic everywhere [image]



(10) Introducing Star-Star Encounters
So far, we have considered star motion in a perfectly smooth potential
However, in reality, individual stars render this potential bumpy on fine scales
How does this affect the motion of stars --- ie is the "collisionless"
assumption valid ?
(a) Estimating Encounter and Relaxation Timescales
Substituing, we get
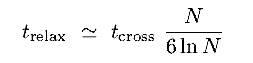 |
(8.38c) |
Surprisingly, this only depends on N, the total number of stars in the
system
Notice that trelax > tcross for
N 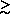 30
30
 to good approximation, stars usually orbit in the overall potential
to good approximation, stars usually orbit in the overall potential
Equal logarithmic intervals in b contribute equally to long term
deflection.
E.g. the ranges : R to ½R ; ½R to ¼R ; .......
2bmin to bmin all contribute equally
However, since the deflection drops rapidly with b as 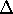 V / V
V / V 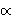 1 / b
1 / b
 for systems with R >> bmin most scattering is due to
weak encounters (
for systems with R >> bmin most scattering is due to
weak encounters (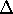 V << V)
V << V)
Example :
Galaxy with R ~ 10 kpc ; bmin ~ 1 AU (1 M stars); so ln
stars); so ln 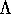 = 20
= 20
Half deflection from encounters outside b1 where ln R/b1 = 10
3/4 deflection from encounters outside b2 where ln R/b2 = 15
b1 = 0.5 pc for which 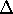 V / V =
bmin / b1
V / V =
bmin / b1 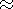 10-5
10-5
b2 = 0.003 pc for which 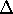 V / V =
bmin / b2
V / V =
bmin / b2 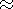 0.15%
0.15%
Need care with N-Body simulations when N << Nstars
 is more grainy than reality, and
trelax(simulation) << trelax(reality)
is more grainy than reality, and
trelax(simulation) << trelax(reality)
Avoid by softening star potentials to increase bmin
Care: lose structure on scales R < bmin
(b) Timescales for Real Stellar Systems
- Here are rough timescales (in years) for a number of stellar systems :
| System |
N |
R (pc) |
V (km/s) |
tcross |
trelax |
tage |
age/relax |
| Open Cluster |
102 |
2 |
0.5 |
106 |
107 |
108 |
10 |
| Globular Cluster |
105 |
4 |
10 |
5 ×105 |
4 ×108 |
1010 |
20 |
| Dwarf Galaxy |
109 |
103 |
50 |
2 ×107 |
1014 |
1010 |
10-4 |
| Elliptical |
1011 |
104.5 |
250 |
108 |
4 ×1016 |
1010 |
10-7 |
| Spiral Disk |
1011 |
104.5 |
20 |
1.5 ×109 |
6 ×1017 |
1010 |
10-8 |
| MW Nucleus |
106 |
1 |
150 |
104 |
108 |
1010 |
100 |
| Luminous Nucleus |
108 |
10 |
500 |
2 ×104 |
1010 |
1010 |
1 |
| (Galaxy Cluster) |
102 |
5 ×105 |
500 |
109 |
(3 ×109) |
1010 |
(3) |
-
The presence of dark matter complicates the situation in clusters (see
[Topic 13.4c])
In practice, 2-body relaxation is not as fast as our simple analysis
suggests.
-
2-Body relaxation may be relevant for star clusters and galaxy nuclei.
-
For most galaxies, 2-body relaxation is utterly negligible.
Because this course deals specifically with galaxies (and not star clusters)
We will only briefly consider the ramifications of relaxation.
-
Don't forget, relaxation times can vary greatly within a given system
For example, a GC core can be relaxing while the halo is not.
(c) Analytic Treatment : The Fokker-Planck Equation
-
You may be wondering when Max Planck (& Adriaan Fokker) worked on stellar
dynamics....
They didn't : much of this work has its roots in plasma physics
Unlike neutral gases, charges in plasmas have long range Coulomb interactions
The early work on plasmas has been appropriated and applied to stellar systems
-
For a smooth potential, the DF obeys the CBE : df / dt = 0
With encounters, stars scatter into and out of the phase space
trajectory: df / dt = 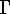 (f)
(f)
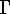 (f) is a collision term and itself
depends on f
(f) is a collision term and itself
depends on f
-
If the full collision term is included we have the master equation.
If most scatterings are distant, an approximation for the collision term yields the Fokker-Planck equation.
This is a PDE, for which several approaches to solutions have been made (see B&T-2 7.4).
(d) Results : The Effects of Encounters
There are a number of distinct phenomena which result from 2-body encounters:
(i) Relaxation
-
2-body relaxation introduces the equivalent of thermal conduction in a gas
For self-gravitating systems, this can be a rather interesting process
Recall from [§8.5e]
that such systems have negative specific heat
 if you remove energy (heat), stars fall deeper in the gravitational well
if you remove energy (heat), stars fall deeper in the gravitational well
 they therefore speed up, and that part of the system gets hotter
they therefore speed up, and that part of the system gets hotter
-
In its simplest form, this relaxation renders clusters more centrally
concentrated
 stellar encounters in the core pass energy to envelope stars
stellar encounters in the core pass energy to envelope stars
 the core contracts and heats, the envelope expands and cools
the core contracts and heats, the envelope expands and cools
After some time the envelope develops a density
profile  (r)
(r)
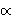 r-3.5
r-3.5
Radial anisotropy increases with time and radius
(stars kicked out from encounters in the core, so carry little AM)
A successful DF is due to Michie, and is f(E,L) 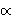 exp(-L2/Lo2) × [exp(E /
exp(-L2/Lo2) × [exp(E /  2) - 1]
2) - 1]
-
After about 15 trelax, the process takes off in a runaway gravothermal catastrophe
(An intuitive explanation is tricky -- see B&T-2 7.3.2)
This "event" is called core collapse and leaves a density law
 (r)
(r)
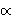 r-2.23 (infinite at r=0 !)
r-2.23 (infinite at r=0 !)
Since GC are about 20 × trelax old, at least some have
probably undergone core collapse
In practice, core collapse is not as dramatic as its name suggests :
Either
- The core "runs out of stars" before densities become exotic
- A hard binary forms which
 (a) ejects stars from the system, accelerating evaporation
(a) ejects stars from the system, accelerating evaporation
 (b) scatters core stars, heating the core and halting core collapse
(b) scatters core stars, heating the core and halting core collapse
(binary acts like nuclear burning in a star)
(ii) Equipartition
-
Violent relaxation during formation leaves all stars the same velocity
distribution
Consequently heavier stars have more kinetic energy.
This is unlike a gas, where molecules have the same kinetic energy (heavier ones move slower).
-
2-body encounters mimic molecular interactions: energy passed from
high mass to low mass stars
In the limit of complete interaction, energy is shared equally (hence equipartition)
-
More massive stars begin to sink deeper
 mass segregation.
mass segregation.
Probably occurred in GCs, though difficult to check since (visible) giants
all have similar mass.
May have played role in galaxy clusters, but complicated by other effects (dynamical
friction, mergers).
(iii) Escape (Ejection and Evaporation)
-
Encounters can result in stars with V > Vesc
This can occur in two ways :
A single encounter gives the star sufficient energy to escape (ejection)
A star slowly wanders into unbound phase space due to many distant encounters
From the analysis above (10.a.iii), the second is much more important
-
Using the fact that Vesc2 = -2
 (r), it is easy to show (B&T p 490) that
<Vesc2> = 4 <V2>
(r), it is easy to show (B&T p 490) that
<Vesc2> = 4 <V2>
So the rms escape velocity is just twice the rms velocity
For a Maxwellian, the fraction with V > 2Vrms = 7 ×10-3
So this fraction is lost every trelax  tevap
tevap
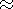 140 trelax
140 trelax
-
The process speeds up in a galaxy tidal field, since Vesc is reduced (see
[Topic 12.3.b])
-
Evaporation + equipartition
 less massive
stars evaporate first (higher velocities).
less massive
stars evaporate first (higher velocities).
Explains unusually low M/L (~2) for GCs compared to other pop II objects (M/L ~ 10).
-
The observed distribution of trelax for the ~150 MW GCs
shows essentially none < 108 years
Selection effect: since tevap ~ 100 trelax
these GCs have probably already evaporated
Suggests young MW may have had many more GCs


(11) Further Topics
We defer a few topics of Stellar Dynamics to later sections :







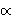 G
G 
 dr / r2
dr / r2  equal force from all distances
equal force from all distances 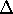 V ~ V)
V ~ V) 
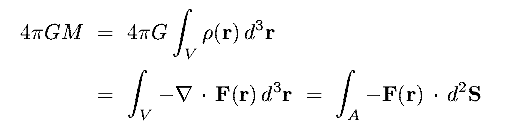
 = 0 at r =
= 0 at r =  we
get (B&T-2 p 59) :
we
get (B&T-2 p 59) :
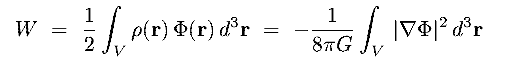

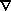
 G
G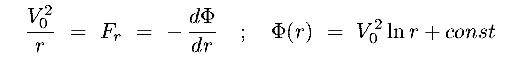
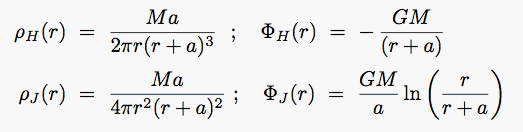
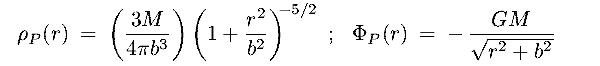

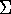
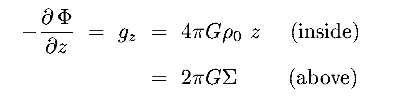
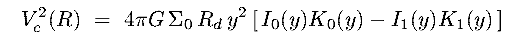


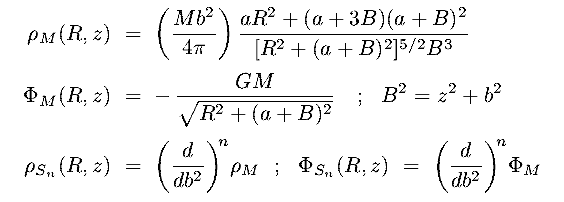
 sums of spherical
shells of non-uniform surface density.
sums of spherical
shells of non-uniform surface density. 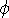 = 0 in spherical polar coordinates
= 0 in spherical polar coordinates 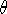 ,
,
 2)-3/2
2)-3/2 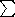 Mj G (
Mj G (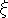 = K / |W| (note K is always +ve, W always -ve)
= K / |W| (note K is always +ve, W always -ve)

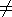 1 (using rp Vp = ra Va from AM conservation)
1 (using rp Vp = ra Va from AM conservation)
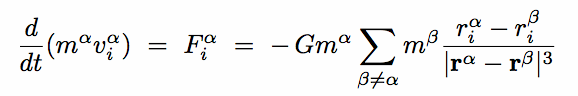
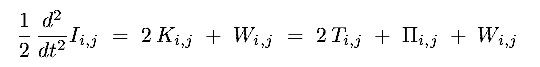
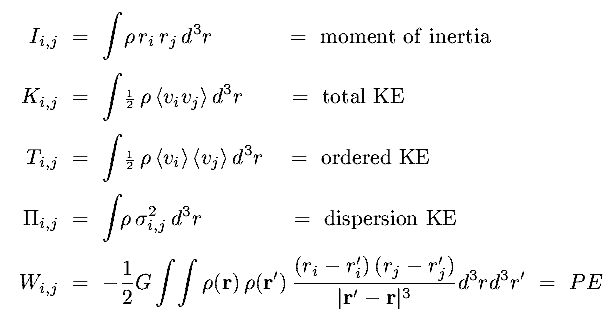
 i,j arises from the expansion: <vi vj> = <vi><vj> +
i,j arises from the expansion: <vi vj> = <vi><vj> + 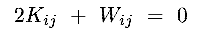
 )
) 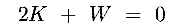

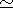 Rm / 0.4
(note Rm is written rh in B&T)
Rm / 0.4
(note Rm is written rh in B&T)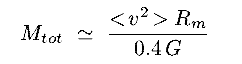
 × 107 years,
× 107 years, 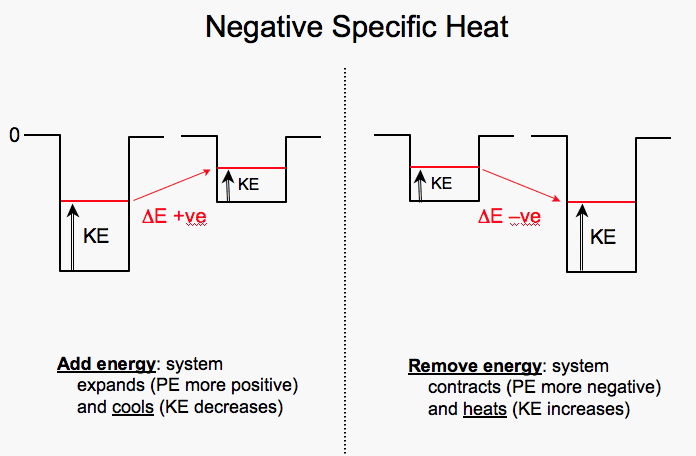
 to z)
to z) 
 )
)  (A/B)0.9 = (1 -
(A/B)0.9 = (1 - 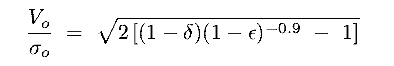

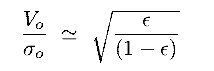


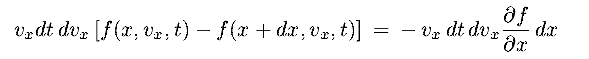
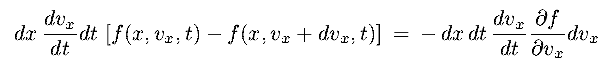
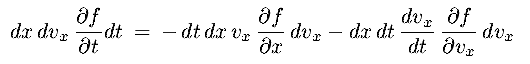
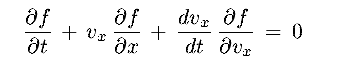
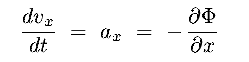
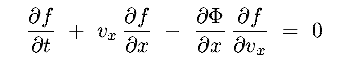
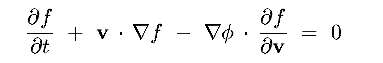
 f/
f/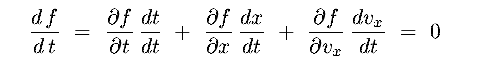
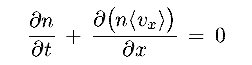
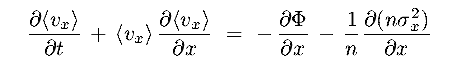
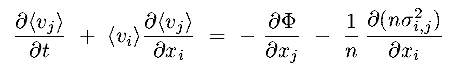

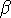 )
) 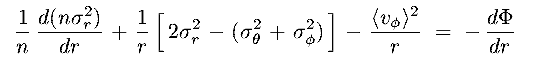
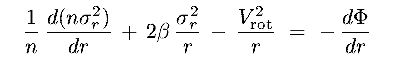
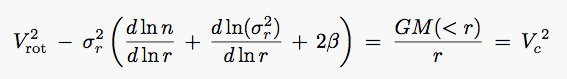
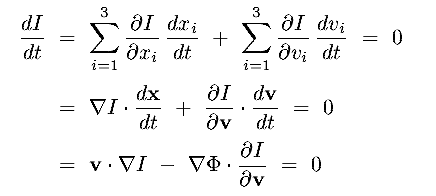
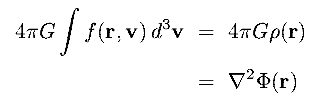
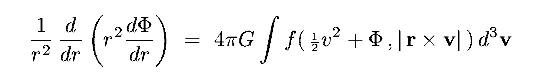
 =
=  (2
(2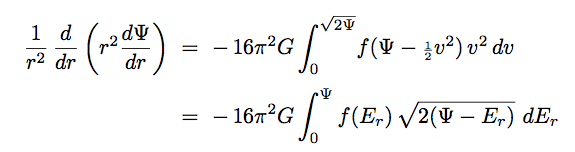
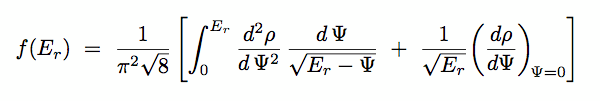
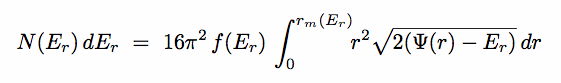
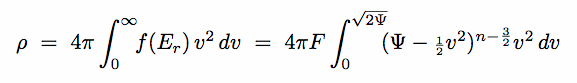
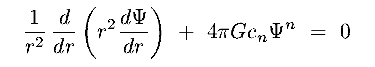
 )
) 

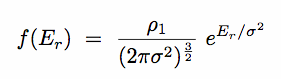
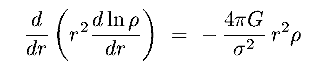
 we have
we have


 15 ro)
15 ro) 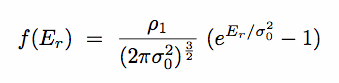
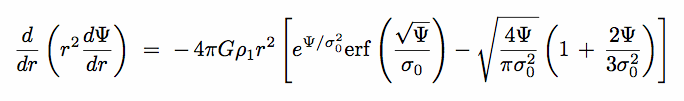




 for earth's orbit
for earth's orbit 
 acceleration
acceleration 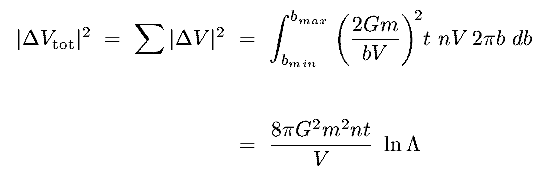
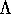 = bmax / bmin
= bmax / bmin
 , and
, and
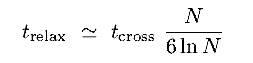
 (f)
(f)