La densité de puissance (intensité du champ)
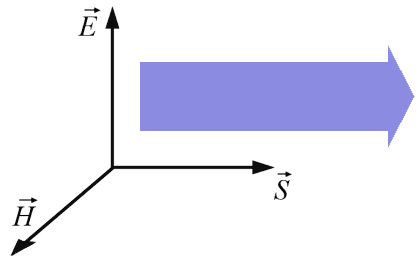
Figure 1 : Vecteur du champ électrique
Figure 1 : Vecteur du champ électrique
Du courant alternatif passant dans un conducteur produit un champ électromagnétique. Si un générateur entretien ce courant dans un circuit ouvert, le champ se propage dans l’espace libre au bout du fil (voir la technologie des antennes). Pour calculer l'énergie contenue dans le champ électromagnétique il faut mesurer l'intensité des champs électriques (E) et magnétiques (H). Chacune de ces deux variables est un vecteur qui varie dans l’espace et le temps.
Le vecteur de propagation de l’énergie électromagnétique se dirige perpendiculairement à E et H, et se nomme le vecteur de Poynting (S). Si l’onde électromagnétique prend la forme d’un sinus à une fréquence précise, le vecteur S oscille et prend toujours la direction de propagation. Il donne la puissance de rayonnement par unité de surface, c'est à dire la quantité d'énergie électromagnétique qui coule par seconde perpendiculairement à la direction de propagation de S par m².
Mathématiquement, cela est décrit par le produit vectoriel de E et H:
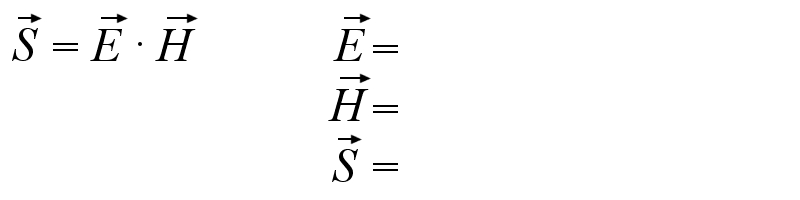
Le produit vectoriel donne des volt-ampères par mètre carré, soit une unité d’énergie par mètre carré.
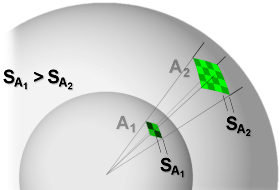
Figure 2 : La densité de puissance isentropique diminue comme le carré de la distance.
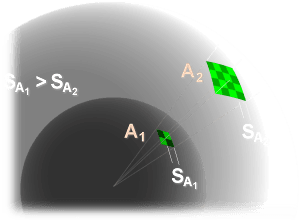
Figure 2 : La densité de puissance isentropique diminue comme le carré de la distance.
Si l’énergie d’ondes haute fréquence est émise de façon isentropique, elle se répand uniformément dans toutes les directions sur une sphère, centrée sur l’émetteur, qui s’élargit constamment (Surface = A = 4 π R2). La densité d’énergie S est donc inversement proportionnelle au rayon de la sphère au carré (1/R2) pour le récepteur, selon l’affaiblissement de propagation dans le vide. L’atténuation par l’atmosphère (air, précipitations, nuages, etc.) diminue le signal encore plus. Par contre, la diminution pour H est linéaire, donc en 1/R:
| P = P0· | 1 | ; | H = H0· | 1 | (2) |
| R2 | R |
