Affaiblissement en espace libre
En télécommunications, l’affaiblissement en espace libre (FSL) est la diminution idéale par propagation d'un signal à l'intérieur d'un espace où il n'y aurait que les deux antennes d'émission et de réception. Ce phénomène ne dépend que de la distance parcourue dans le vide de l’espace, comme entre deux satellites, mais il est affecté par d’autres facteurs dans l’atmosphère. Il est un des paramètres de l’équation radar.
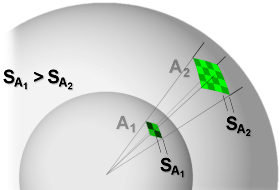
Figure 1 : Densité de puissance isotrope diminuant géométriquement.
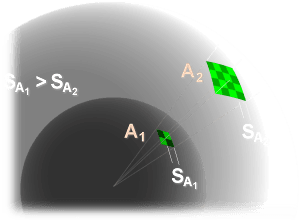
Figure 1 : Densité de puissance isotrope diminuant géométriquement.
Calcul de l’affaiblissement
L’énergie d’un émetteur haute-fréquence isotrope se répartit également dans toutes les directions. La densité d’énergie est donc la même sur une sphère ayant un rayon R et dont la surface est ( A= 4πR² ). Comme il n’y a pas de production d’énergie ailleurs qu’à la source, l’énergie émise à un temps t se disperse à l’infini et la densité diminue inversement à l’augmentation de R..
L’expression de l’affaiblissement en espace libre englobe deux effets. Le premier est la diminution avec la distance de l’émetteur, soit inversement proportionnel à R². Le second est que cette diminution est proportionnelle au carré de la longueur d’onde émise.
Le premier terme s’exprime comme :
| S = | Pt | en [W/m2] |
Pt = puissance transmise [Watts] S = densité de puissance par unité de surface à R R = Distance transmetteur – récepteur [mètres] |
(1) |
| 4 · π · R2 |
Le second est relié à l’ouverture de l’antenne, ce qui décrit jusqu’à quel point l’antenne peut capter le signal électromagnétique. Pour une antenne isotrope, la puissance reçue est :
| Pr = | S · λ2 | en [W] |
Pr = puissance reçue S = densité de puissance isotrope λ = longueur d’onde |
(2) |
| 4 · π |
L’affaiblissement total est obtenu en combinant les deux effets par :
| FSL = | Pt | = | (4 · π · R)2 | = | (4 · π · R · f )2 | fr = fréquence transmise c = vitesse de la lumière dans le vide, 2,99792458 · 108 mètres par seconde |
(3) |
| Pr | λ2 | c2 |
