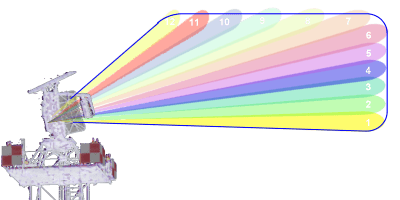
Antenne à faisceau en cosécante carrée
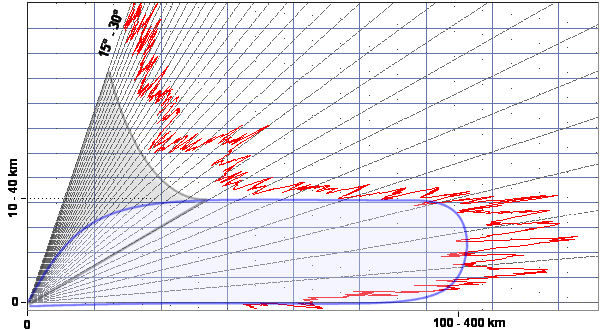
Figure 1 : Diagramme d’émission dans la verticale d’une antenne à faisceau en cosécante carrée²
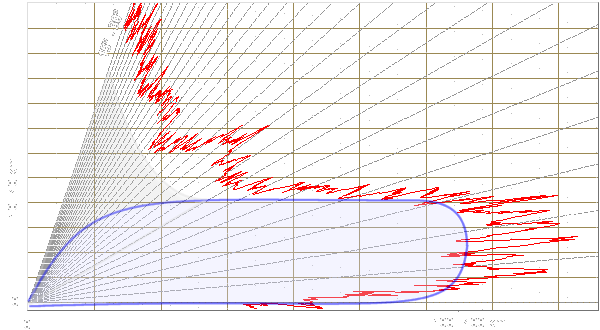
Figure 1 : Diagramme d’émission dans la verticale d’une antenne à faisceau en cosécante carrée²
Une antenne à faisceau en cosécante carrée est spécialement prévue pour la surveillance aérienne. Elle permet de répartir dans la verticale l’énergie émise afin de sonder un maximum d’angles d’élévation sans avoir à faire des balayages angulaires multiples. Ce diagramme d’émission permet d’obtenir une rétrodiffusion relativement constante de la cible si celle-ci demeure à la même altitude et variable si elle en change, selon le diagramme d’émission connu de l’antenne (voir section sur sa formulation mathématique).
Il existe deux variantes de ce type d’antenne:
- antenne parabolique déformée;
- un empilement de cornet d’alimentation autour du point focal d’une parabole.
La première méthode consiste à déformer d’utiliser une antenne parabolique dont on change la courbure dans sa partie supérieure. Le cornet émetteur est placé au point focal de la parabole et le faisceau provenant de la partie paraboloïde est formé d’ondes parallèles concentrées et est appelé le « lobe principal ». La partie du haut a une courbure moins grande et dirige les ondes à un certain angle par rapport à l’horizontale comme dans la figure 2 a. On peut aussi augmenter la courbure du bord inférieure du réflecteur, cela a le même effet. Avec ces deux méthodes, l’énergie émise par les bords déformés est diffluente et donc la puissance émise vers les cibles est plus faible qu’avec le lobe principal, ce sont des « lobes secondaires ». L’énergie retournée à de forts angles de site (ou d’élévation) est donc plus faible ce qui en limite la portée.
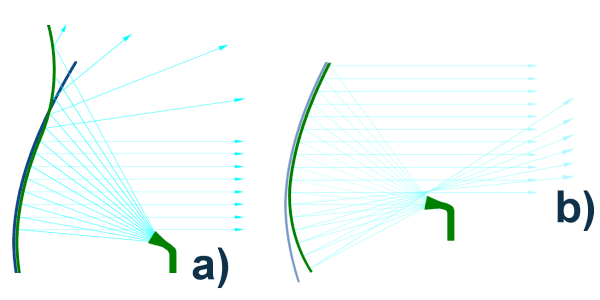
Figure 2 : Les deux type d’antennes à faisceau en cosécante carrée
a) Parabole déformée dans sa partie supérieure
b) Parabole déformée dans sa partie inférieure
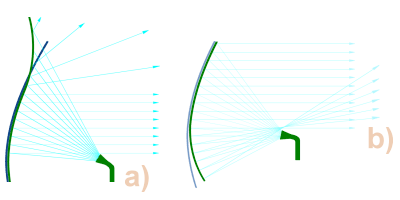
Figure 2 : Les deux type d’antennes à faisceau en cosécante carrée
a) Parabole déformée dans sa partie supérieure
b) Parabole déformée dans sa partie inférieure
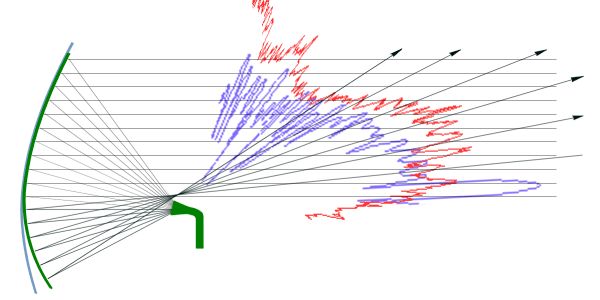
Figure 3 : Diagramme d’émission en cosécante carrée en augmentant la courbure du bord inférieur de la parabole.
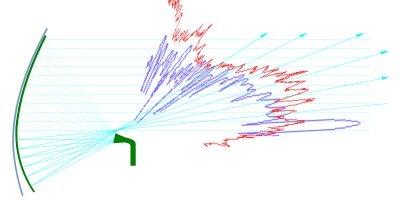
Figure 3 : Diagramme d’émission en cosécante carrée en augmentant la courbure du bord inférieur de la parabole.
Empilement de cornet
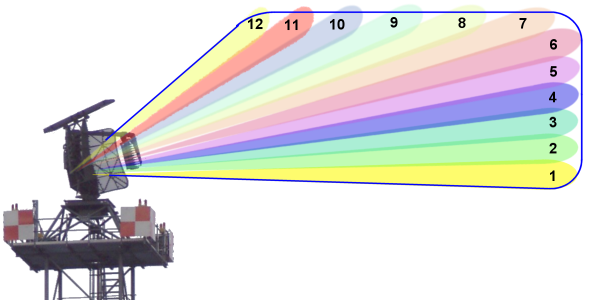
Figure 4 : Empilement de cornet d’alimentation qui donne une cosécante carrée

Figure 5 : Empilement de douze cornets d’émission d’un radar ASR 910 pour obtenir un diagramme en cosécante carré

Figure 5 : Empilement de douze cornets d’émission d’un radar ASR 910 pour obtenir un diagramme en cosécante carré
Le second type est celui qui est obtenu en empilant une série de cornet d’émission autour du point focal de l’antenne parabolique. Chaque cornet donne un faisceau parallèle mais avec un angle par rapport à l’horizontal qui dépend de sa position. Si l’énergie est distribuée inégalement entre les cornets, on peut obtenir un diagramme d’émission proche d’une cosécante carrée. Dans ce cas, chacun des cornets peut utiliser une fréquence différente ou une phase différente ce qui permet de reconnaître à la réception la provenance du signal de retour et donc l’élévation de la cible. Cela est similaire à faire plusieurs balayages en élévation en une seule fois.
Finalement, le diagramme en cosécante carrée peut être réalisé avec d’autres réflecteurs que paraboloïde. Le faisceau direct d’une antenne réseau formée de plusieurs antennes Yagi peut être mélangé au signal venant de la réflexion au sol pour obtenir le même résultat (voir l’ellipsoïde de Fresnel).
Diagramme en cosécante carrée
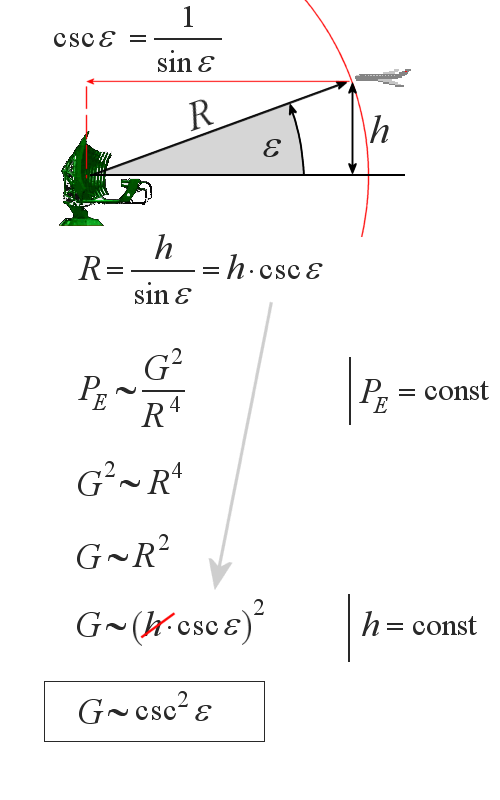
Le terme cosécante provident de la formule trigonométrique du même nom (Cosec).
La hauteur h et la distance de la cible R détermine son angle de site (ou d’élévation) ε.
On sait d’abord que le sinus d’un angle est h/R, en remplaçant dans la formule de la cosécante, on obtient
On sait par
l’équation radar
que Pe est proportionnelle au gain au carré (G2)
sur R4 :
En utilisant l’hypothèse que la puissance émise Pe est une constante,
G devient proportionnel à R2.
En remplaçant, R par la cosécante de ε et en considérant h
comme une constante, on obtient que le gain est proportionnel à la cosécante carré ε pour que la puissance soit constante.
Cela correspond à ce qui avait été mentionné en début de page
« Ce diagramme d’émission permet d’obtenir une rétrodiffusion relativement constante de la cible si celle-ci demeure à la même altitude. »