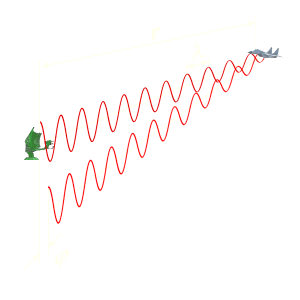
Effet Doppler-Fizeau
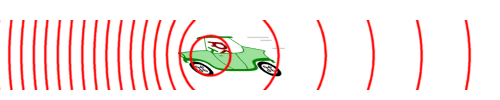
Figure 1 : Effet Doppler-Fizeau
Effet Doppler-Fizeau
L'effet Doppler est le décalage de fréquence d’une onde acoustique ou électromagnétique entre la mesure à l'émission et la mesure à la réception lorsque la distance entre l'émetteur et le récepteur varie au cours du temps. Cet effet fut découvert par le physicien autrichien Christian Doppler en 1842 et fut également proposé par Hippolyte Fizeau pour les ondes électromagnétiques en 1848.
L’effet Doppler Fizeau est utilisé par un radar pour deux tâches :
- Mesure de la vitesse des cibles ;
- Filtre des faux échos pour la Visualisation des cibles mobiles.
Pour comprendre ce phénomène, il s’agit de penser à une onde à une fréquence donnée qui est émise vers un observateur en mouvement, ou vis-versa. La longueur d’onde du signal est constante mais si l’observateur se rapproche de la source, il se déplace vers les fronts d’ondes successifs et perçoit donc plus d’ondes par seconde que s’il était resté stationnaire, donc une augmentation de la fréquence. De la même manière, s’il s’éloigne de la source, les fronts d’onde l’atteindront avec un retard qui dépend de sa vitesse d’éloignement, donc une diminution de la fréquence.
Dans le cas sonore, cela se traduit par un son plus aigu lors d’un rapprochement de la source et un son plus grave en s’éloignant de celle-ci. Dans le domaine de la lumière visible, on parle de décalage vers le bleu pour un rapprochement et vers le rouge dans le cas d’éloignement en se référant au spectre lumineux. La même chose s’applique à toutes les gammes d’ondes électromagnétiques dont les ondes utilisées par les radars.
En termes mathématiques, la variation de fréquence peut être exprimée par:
| fD = | 2·vr | fD = Fréquence Doppler [Hz] λ = Longueur d’onde [m] vr = vitesse relative source-observateur [m/s] |
|
| λ |
La vitesse vr est la composante radiale de la vitesse réelle de l’observateur car la variation de fréquence est due au déplacement relatif entre la source et l’observateur. La composante tangentielle de la vitesse réelle n’implique pas d’éloignement ou de rapprochement et donc ne peut pas être perçue. Ainsi, un radar qui sonde l’atmosphère ne peut percevoir que la composante radiale de sa vitesse par l’effet Doppler. Pour connaître sa vitesse complète, il faut noter sa position angulaire entre chaque sondage ce qui donne la composante tangentielle.
| fD = | 2·v | · cos α | fD = Fréquence Doppler [Hz] λ = longueur d’onde [m] v = vitesse de la cible [m/s] α = angle entre l’axe radar-cible et celle de déplacement reel de la cible |
|
| λ |
La vitesse Doppler par paire d’impulsions
La mesure de fD est relativement faible par rapport à la longueur d’onde pour les vitesses habituelles mesurées par un radar. Pour un radar à onde continue, la différence de fréquence peut être donnée en procédant à un mélange entre l’onde émise et celle retournée ce qui cause un battement à fD qui peut être mesuré.
Par contre, dans le cas d’un radar à impulsions cela n’est pas possible car la mesure directe de fD est la plupart trop petite pour les instruments. Dans ce cas, c’est la différence de phase entre impulsions successives qui est utilisé. En effet, si la cible se déplace par rapport au radar entre deux impulsions, l’onde devra parcourir un plus long chemin ce qui donnera une différence de la phase φ. Le déphasage maximal qu’on peut avoir entre deux ondes identiques étant de 360° avant que les deux ne se superposent à nouveau:
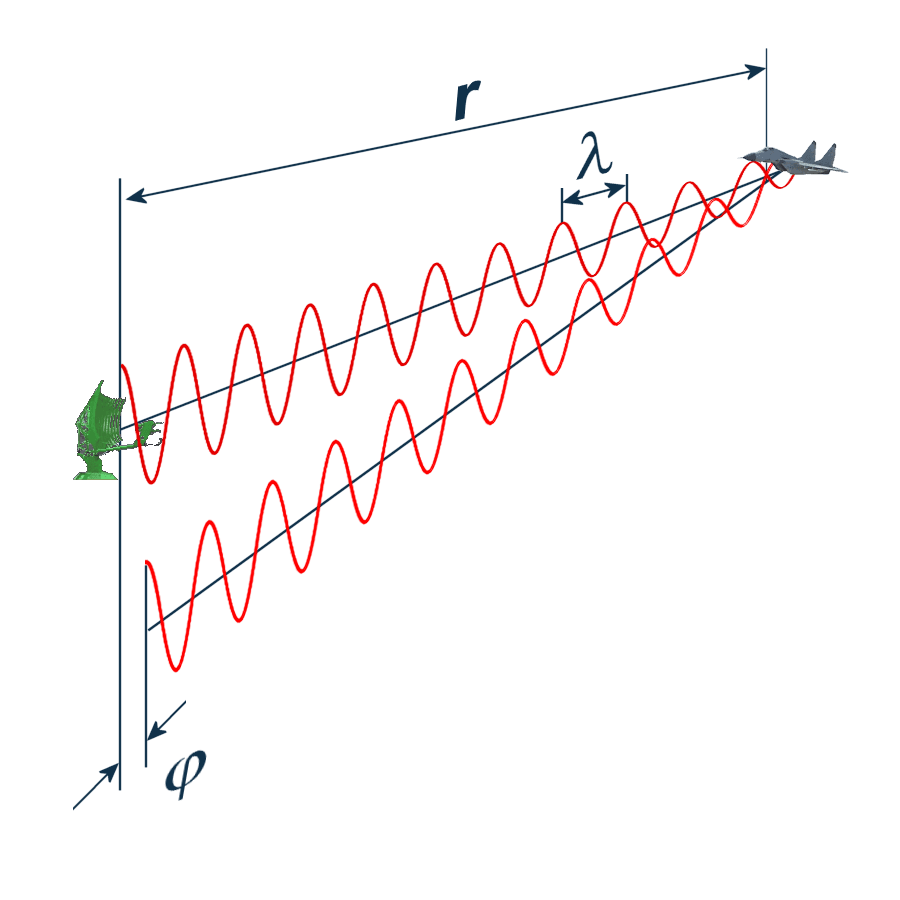
Figure 2 : Le déphasage entre les impulsions.
| φ = − | 2r · 2π | φ = déphasage entre le signal émis et celui reçu 2r = la distance aller-retour à la cible 2π = 360° est le déphasage maximal λ = longueur d’onde du faisceau radar |
| λ |
Or vitesse radiale est:
| vr = | d(r) |
| dt |
En remplaçant d(r) dans φ:
| d(φ) | = | - 4π · vr |
| dt | λ |
Le déphasage φ est relié à fD par:
| fD = | 1 | · | d(φ) | = | 1 | · | - 4π · vr |
| 2π | dt | 2π | λ |
| | fD| = | 2 · vr | = | 2 · vr· ftx | where: | ftx = fréquence transmise c0 = vitesse de la lumière vr = vitesse radiale de la cible |
| λ | c0 |
Cette équation démontre que la variation de fréquence Doppler fD est deux fois celle qui serait perçue par la cible. En effet, l’onde subit une variation à l’aller, est réfléchie vers le radar et subit une seconde variation au retour.