Pertes par Fluctuation
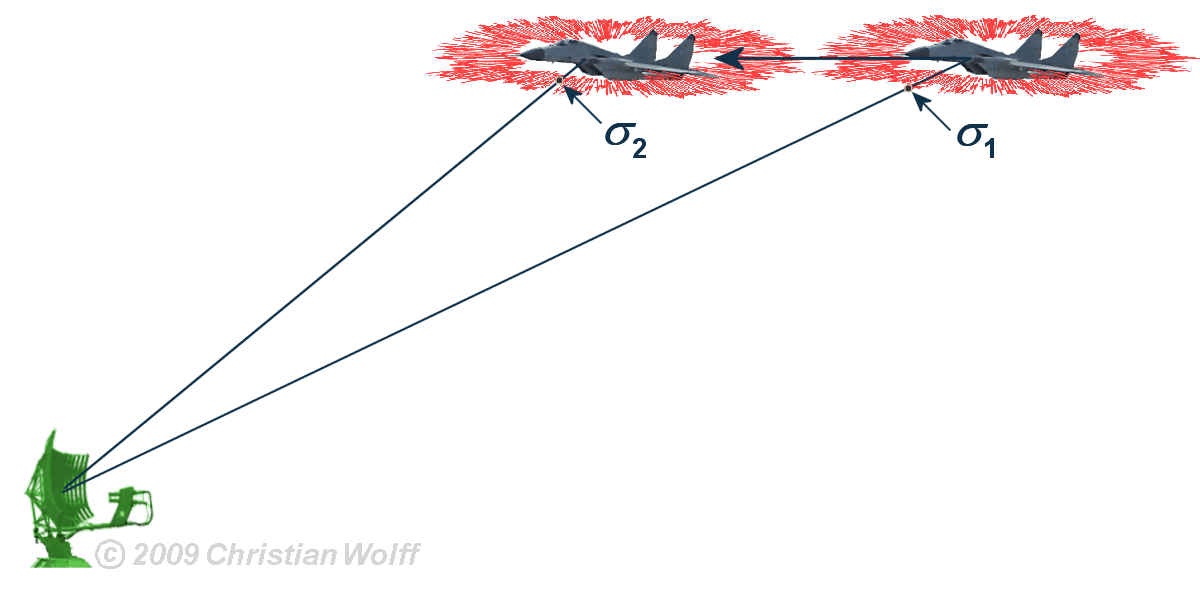
Figure 1 : Fluctuation de la surface équivalente radar due au mouvement de la cible.
Pertes par Fluctuation
Les variations de l’intensité du signal rétrodiffusé par les cibles est dû au changement de la surface équivalente radar (σ) qu’elles présentent au radar lors de leur mouvement. En effet, lorsqu’un avion se déplace, comme dans la figure1, il présente un profil qui varie dans le temps selon son angle par rapport au radar. De plus, les ondes provenant de ses différentes surfaces qui le composent, vont interférer différemment entre elles.
Modèles de Swerling
Les modèles de Swerling ont été développés par le mathématicien américain Peter Swerling et publiés en 1954. Il s’agit de formules mathématiques pour décrire les propriétés statistiques de la surface efficace de formes complexes. Selon Swerling, la densité de probabilité de détection des cibles est décrite par une fonction en Khi carré (χ2) ayant un nombre fini de degrés de liberté (m):
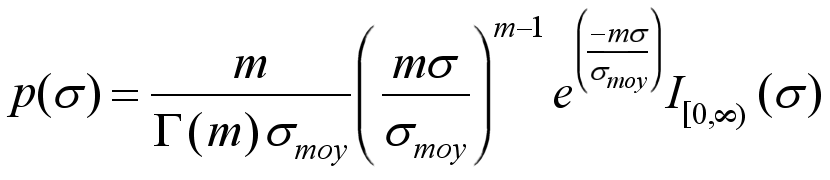
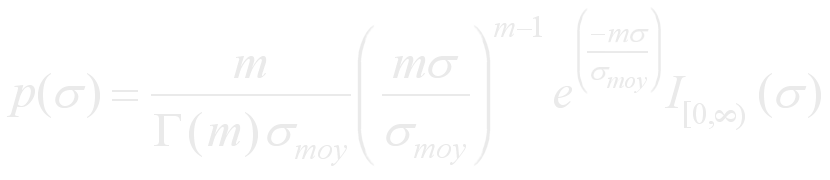
Ces modèles sont particulièrement importants pour calculer σ d’une cible radar théorique. Il y a cinq variantes :
- Swerling I décrit les cibles ayant une rétrodiffusion assez constante durant le
temps d’illumination.
La probabilité de détection varie selon une fonction en Khi carré (χ2)
ayant deux degrés de liberté (m = 1).
La surface équivalente radar est constante d’une impulsion à la suivante lors d’un balayage mais varie de balayage en balayage.
La densité de probabilité de σ est donnée par la
fonction de Rayleigh
suivante
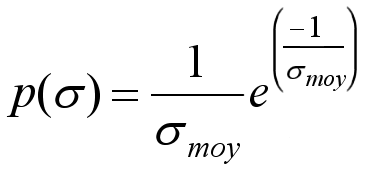
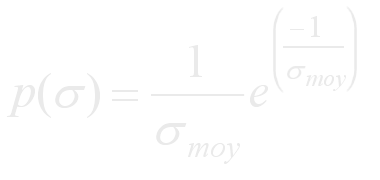 (44)
(44)
Où σmoy est la moyenne arithmétique des values de σ de la cible. - Swerling II est similaire au précédent et utilise la même équation mais σ change plus rapidement et d’une impulsion à la suivante.
- Swerling III est le même que Swerling I mais avec 4 degrés de liberté (m = 2).
La fluctuation de balayage en balayage radar suit la probabilité:
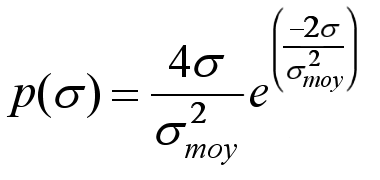
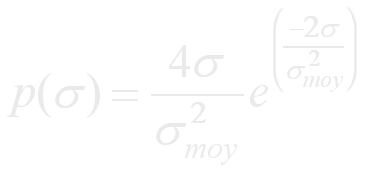 (45)
(45) - Swerling IV: est similaire à Swerling III mais σ varie d’une impulsion à l’autre plutôt que d’un balayage au suivant. On utilise toujours l’équation 45.
- Swerling V: décrit le comportement d’une cible avec un σ constant (aussi connu comme Swerling 0). Il s’agit d’une cible idéale n’ayant pas de fluctuations (m→∞).
Les cas I et II de Swerling s’appliquent à des cibles ayant un grand nombre de diffuseurs indépendants et ayant des surfaces à peu près égales, comme les avions. Les cas III et IV approximent des objets ayant une large surface de rétrodiffusion et plusieurs de petites dimensions, comme des navires. Peter Swerling a démontré que les pertes additionnelles par fluctuation dépendent plus de la probabilité de détection et moins de la probabilité de fausses alarmes PN.
La valeur maximale théorique de détection radar est souvent obtenue par les équations de Swerling II et IV. La perte par fluctuation d’une cible au mouvement régulier est typiquement faible, de l’ordre de 1 à 2 dB, à une probabilité de détection PD=60%.
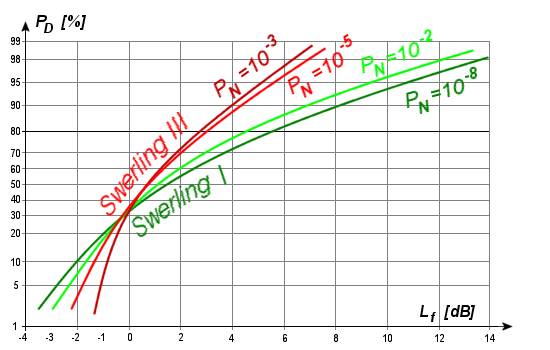
Figure 2 : Perte par fluctuation (Lf) des cas I et III de Swerling.
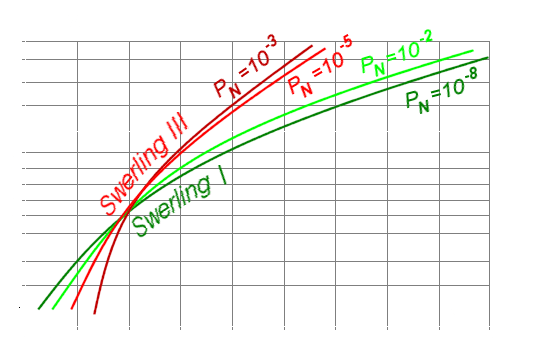
Figure 2 : Perte par fluctuation (Lf) des cas I et III de Swerling.
Les cas I and III s’appliquent aux radars de poursuite. La perte par fluctuation dépend la probabilité de détection selon les courbes de la figure 2. Il y a une forte fluctuation du gain pour PD<30% car l’intensité du signal est alors près de celle bruit.
Source: Swerling, « Probability of Detection for Fluctuating Targets », Rand Research Memorandum RM-1217, 17 mars 1954

