Détecteur de phase en sinus et cosinus (I&Q)
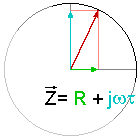
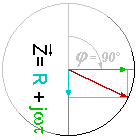
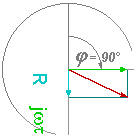
Figure 1 : Parties réelles et imaginaires du signal.
Formulation d’une onde sinusoïdale
L’intensité à un moment donnée d’une onde dépend de la phase à laquelle elle est rendue dans son cycle:
| I(t) = I0 sin(ωt + ϕ) = I0 cos(Φ(t)) + jωt | (1) |
Ici ω est la pulsation et ϕ la phase initiale et
leur combinaison temporelle Φ donne la phase à t et
j est le nombre imaginaire
.
La fréquence intermédiaire de démodulation du signal radar est une telle onde et peut être transformée par un
convertisseur analogue-numérique simple en une série de valeurs d’intensité versus temps.
L’image 1 donne les valeurs réelles du nombre complexe qui représentent cette intensité.
Cependant, l’information sur la phase de l’onde est perdue par cette transformation simple.
Détecteur synchrone
Un nombre complexe a toujours une partie réelle (vert) et une partie imaginaire (cyan). Un convertisseur analogue-numérique ne prend que la partie réelle qui correspond la projection sur l’axe des X.
Ceci n’était pas un problème pour les radars anciens. Le signal était composé d’un train d’au moins 12 à 15 impulsions. Si une ou deux impulsions de retour avaient une amplitude réelle de zéro (maximum de changement de phase), le signal était quand même visible à cause de la séquence des impulsions. Cependant, les nouveaux radars utilisant la technologie monopulse n’émettent qu’une impulsion à la fois et il est donc nécessaire de pouvoir extraire la partie donnant la phase, la partie imaginaire du nombre.
Le détecteur synchrone permet une telle décomposition du signal de la fréquence intermédiaire sans perte d’information. La bande de base du signal en phase (I) et en quadrature de phase (Q) sont numérisés en utilisant une paire de convertisseurs analogue-numériques. Le détecteur synchrone est aussi appelé un récepteur de phase, un détecteur de quadrature de phase, un démodulateur I/Q ou un détecteur cohérent.
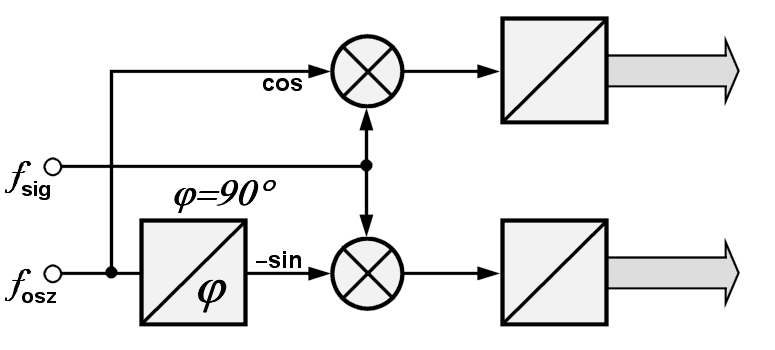
Figure 2 : Schéma du circuit du détecteur synchrone
Figure 3 : Un exemple concret (Document en anglais)
L’idée derrière ce détecteur est tourner le signal de 90°, telle sorte que la partie imaginaire devienne celle qui est projetée sur l’axe des X et puisse être numérisée par le second détecteur. Même si on perd la valeur de la partie réelle, on peut l’extraire grâce au théorème de Pythagore.
Comment effectuer cette rotation? Il s’agit d’introduire un changement de phase de 90° du signal par un déphaseur. Ainsi, le signal du récepteur radar est divisé en deux, le premier signal passe directement dans le convertisseur analogue-numérique (A/N) et le second passe par le déphaseur avec le second convertisseur, comme sur la figure 2.
Les deux données de sortie peuvent ensuite être traitées par un logiciel approprié. Les composantes I et Q sont reliées entre elles par:
| I = A cos(Φ) Q = A sin(Φ) |
(2) |
Φ est la phase de l’onde vidéo venant du récepteur et l’intensité du signal est simplement:
| A2= I2+Q2 | (3) |
La phase Φ sera calculée par:
| Φ = arctan(Q/I) | (4) |
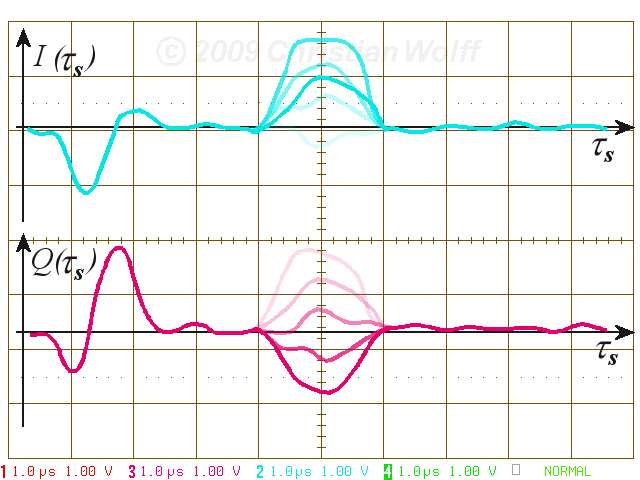
Les signaux en phase (cyan) et en quadrature (magenta)