Les Principes du Radar

Ellipsoïde de Fresnel

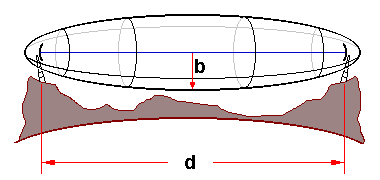
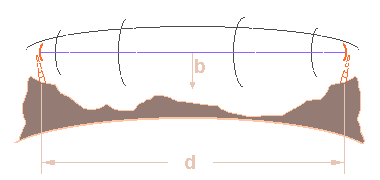
Figure 1 : Ellipsoïde de Fresnel, où « d » est la distance entre les antennes émettrices et réceptrice, « b » le rayon au centre de l’ellipsoïde.

L’ellipsoïde de Fresnel est un volume dans l'espace permettant d'évaluer l'atténuation apportée par un obstacle (immeuble, colline…) à la propagation d'une onde radio. Il est calculé à partir de la diffraction de l’onde par un émetteur hypothétique ayant une ouverture circulaire pour les longueurs d’onde VHF, UHF ou hyperfréquences. La méthode de l'ellipsoïde de Fresnel permet d'évaluer le rayon à l’intérieur duquel se produit l'atténuation le long du trajet de l’onde et de calculer les pertes.

Tout obstacle se trouvant à l’intérieur de l’ellipsoïde reflétera une partie de l’onde de manière diffuse et la partie qui arrivera au récepteur pourra être déphasé par rapport au signal direct. Cela causera des interférences qui affaibliront généralement le signal reçu. Par contre, dans certaines circonstances le signal direct et celui réfléchi sont en phase, donnant un rehaussement du signal.

Pour calculer le rayon de l’ellipsoïde au centre du trajet, là où il est le plus grand, on utilise la formule suivante:

Où d est distance entre le transmetteur et le récepteur, b le rayon et λ la longueur d’onde émise.

Application indirecte au radar

Les radars de très basse fréquence, comme ceux en VHF et transhorizon, utilisent la réflexion sur le sol de leurs lobes secondaires pour augmenter la largeur de leur faisceau principal afin de pouvoir détecter à très basse altitude. Cela implique que le terrain autour du radar soit pratiquement lisse. Par exemple, le radar P–18 (« Spoon Rest D ») a besoin d’utiliser le sol dans un rayon de 1 000 mètres et les obstacles doivent y avoir moins de 1 mètre de hauteur pour ne pas nuire à la réflexion.

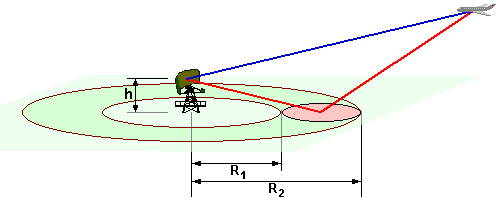
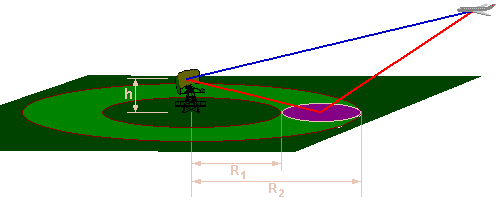
Figure 2 : Application indirecte du principe de Fresnel

Bien qu’il ne s’agisse pas à proprement parler d’une application directe de l’ellipsoïde de Fresnel, le principe est assez similaire et a été appelé « première zone de Fresnel » dans certains articles sur le sujet.

La distance minimale et maximale utilisable pour obtenir cette réflexion est calculé par:

Plus la zone de réflexion est éloignée de l'antenne, plus la hauteur acceptable des aspérités est grande. Les ondes entre R₁ et R₂ sont déphasées de 180° par rapport au faisceau direct, à cause de la réflexion.