Largeur du faisceau
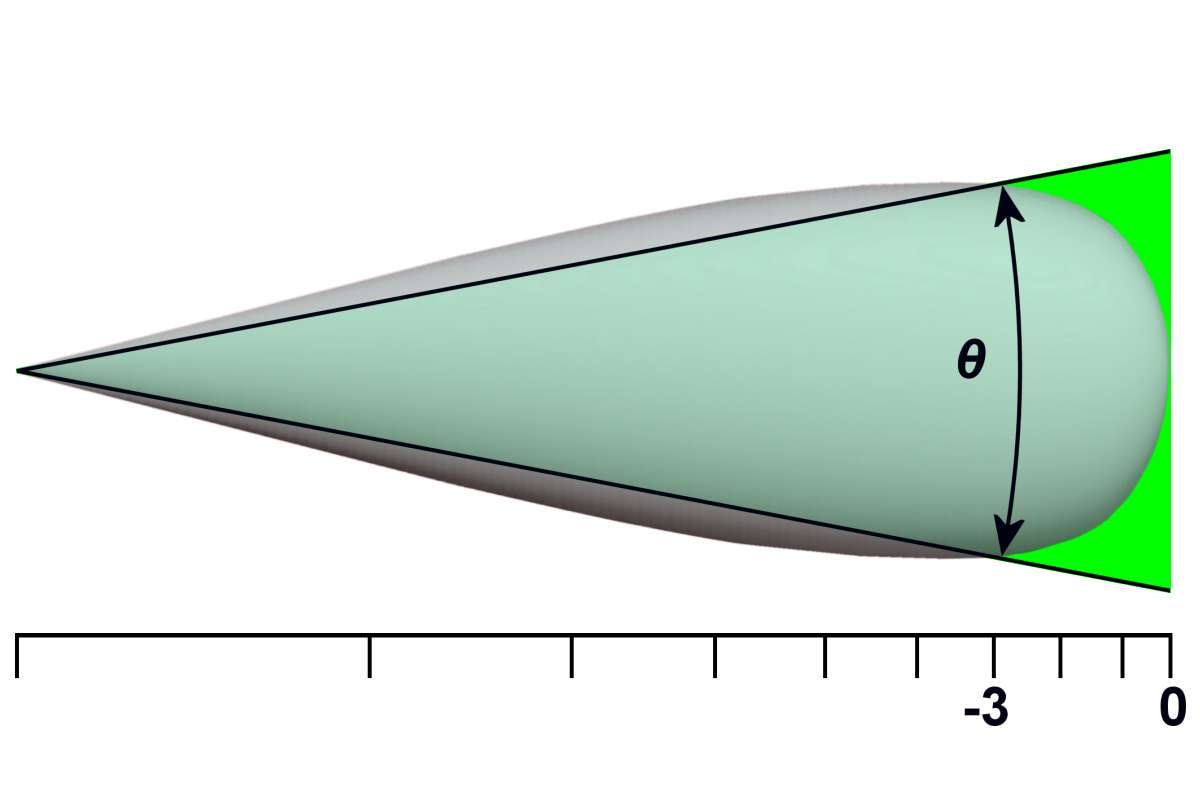
Figure 1 : Largeur du faisceau (θ).
Largeur du faisceau
Par ouverture ou largeur du faisceau de l’antenne radar, on entend généralement l’angle entre l’axe d’émission maximal du faisceau et celui où le signal diminue de moitié en puissance. L'intensité du rayonnement est trouvée par une série de mesures angulaires, la plupart du temps dans une chambre anéchoïque. De ces données on obtient l’axe maximal et les points situés de part et d'autre du pic représentant la moitié de la puissance de l'intensité maximale. La distance angulaire entre ces points à mi-puissance est définie comme la largeur du faisceau[1].
Comme la moitié de la puissance exprimée en décibels est égale à −3 dB, la largeur de faisceau à demi-puissance est parfois appelée largeur de faisceau à 3 dB (θ3) ou largeur de faisceau à demi-puissance. Les largeurs de faisceau horizontales et verticales sont généralement prises en compte.
Afin de permettre la mesure directe de paramètres à partir de formes d'onde d'oscilloscope, il était courant d'utiliser des largeurs mesurées également aux points de demi-tension (-6 dB). Ceci est exprimé dans le nom de variable θ6. Sur le diagramme du diagramme d'antenne, ces points de demi-tension n'ont pas la même position que les points de demi-puissance. En supposant que l'impédance soit la même, la moitié de la tension générera la moitié du courant. La moitié du courant multiplié par la moitié de la tension donne un quart de la puissance, exprimée en décibels -6 dB. Si des mesures de tension RF doivent être utilisées pour estimer l'ouverture de faisceau d'une antenne, les points où la tension est 0,707 fois le pic caractérisent l'ouverture de faisceau à mi-puissance.
Approximations
En première approximation, on suppose que les lobes secondaires de l'antenne peuvent être négligés et que la puissance totale générée par l'émetteur est concentrée dans le lobe principal. Afin de corriger les effets de cette approximation à l'aide de calculs théoriques, le terme « Perte de forme du faisceau ».
Une seconde approximation consiste à supposer que la puissance totale se situe dans la largeur de faisceau d'une demi-puissance de l'antenne et qu'elle est répartie de manière égale dans celle-ci (voir la Figure 1, la zone de couleur verte). D'autre part, il est supposé qu'aucune puissance ne peut être mesurée en dehors de la largeur de faisceau à mi-puissance. S'il est nécessaire de corriger les effets de cette approximation dans le calcul des distances ou des amplitudes de signal, le facteur de largeur de faisceau peut être utilisé.
Grâce à ces approximations, il est possible d'utiliser le gain de l'antenne et la puissance générée par l'émetteur directement dans l'équation radar en tant que paramètre.
Sources et ressorces :
- Hamish Meikle: ''Modern Radar Systems'' Artech House on Demand, 2008, ISBN 978-1-59693-242-5, p. 108 (lien internet)