Pseudo-Pythagore
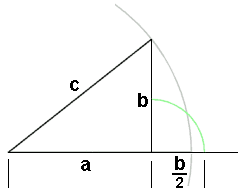
Figure 1 : Théorème de « Pita Gore »
La transformation d’un vecteur en ses composantes orthogonales, projections sur les axes X et Y,
nécessite l’utilisation du théorème de Pythagore.
Malheureusement, le calcul de la racine carrée prend du temps à l’aide de circuits électroniques,
ce qui retarde le traitement des données en temps réel.
Ce délai peut également être variable d’un point à l’autre puisque si a ou b
dans la figure 1 sont nuls, l’hypoténuse est directement connue.
Le tout donnera un temps de traitement inégal des données.
Une approximation, assez précise dans la plupart des cas, est donc utilisée:
La somme du côté le plus long (a) et de la moitié de celui le
plus court (b) du triangle donne approximativement l’hypoténuse (c)
c ≈ a + 0,5 • b
