Détermination de la hauteur par trajets multiples
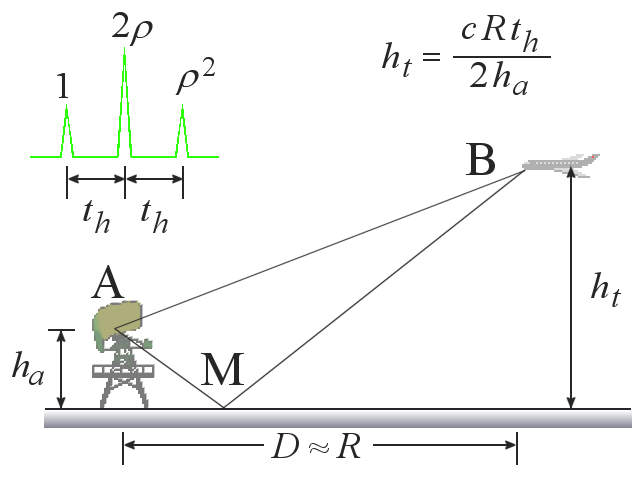
Figure 1 : Détermination de la hauteur d’une cible par trajets multiples (ρ = Coefficient de réflexion)
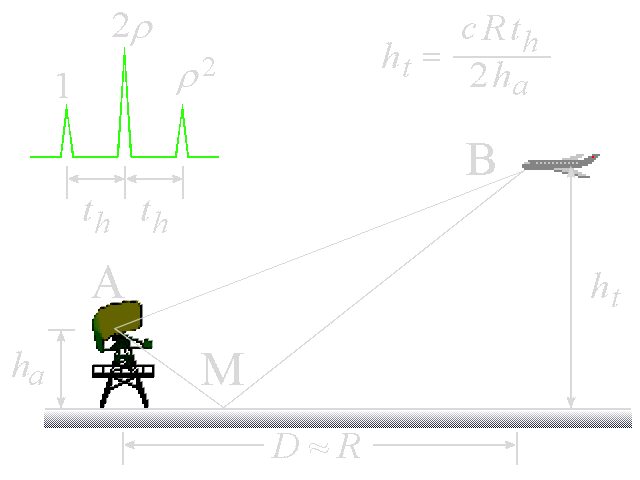
Figure 1 : Détermination de la hauteur d’une cible par trajets multiples (ρ = Coefficient de réflexion)
Détermination de la hauteur par trajets multiples
Dilemme
La hauteur au-dessus du sol est en général trouvée en utilisant un radar sondant en trois dimensions. Ce dernier balaie sur 360 degrés un certain nombre d’élévations avec un faisceau mince appelé « faisceau-crayon ». Ce type de radar est cependant de quatre à dix fois plus coûteux qu’un radar en deux dimensions qui utilisent un faisceau plat ou en cosécante carrée et qui ne peut donner que la distance et l’azimut. De plus, un radar en trois dimensions a une faible résolution aux bas angles d’élévation quand les bords du faisceau peuvent toucher le sol ou la mer.
Trajets multiples
Il est possible d’utiliser la réflexion multiple du faisceau d’un radar en deux dimensions. Ce faisceau est mince horizontalement mais très large verticalement et il détecte toute cible dans une direction donnée grâce au retour direct. Par contre, une partie du faisceau frappe le sol, est réfléchi vers la cible qui retourne de celle-ci vers le radar. Le signal retourné au radar est donc multiple. En prenant comme hypothèse une Terre plate on a :
- le trajet direct AB+BA ;
- le trajet radar-sol-cible-radar AMB+BA ;
- le trajet radar-cible-sol-radar AB+BMA de même longueur que le précédent ;
- le trajet radar-sol-cible-sol-radar AMB+BMA.
Si le radar a une résolution spatiale suffisante, il est possible de déterminer la séparation temporelle entre ces quatre retours par :
| th = | 2ha · ht | où | ha = hauteur de l’antenne radar ht = hauteur de la cible c = vitesse de la lumière R = distance |
(1) |
| c · R |
En replaçant ht /R par sin sin Θe de l’angle de site (d’élévation) :
| sin Θe = | c · th | où | Θe = angle d’élévation th = différence de temps de trajet |
(2) |
| 2 ha |
On obtient la hauteur de la cible:
| ht = | c · R · th | (3) |
| 2 ha |
Par exemple, si ha = 100 pieds et R = 50 milles marins, th sera 6,69 ns ce qui veut dire que la gamme de fréquences que peut percevoir le récepteur du radar doit être d’au moins 149,5 MHz de chaque côté de la fréquence porteuse. Plus l’angle d’élévation (ou de site) vers la cible est grand par rapport au sol, plus grand doit être la séparation en fréquences des échos de trajets multiples et plus il sera donc facile de déterminer th. En pratique, un radar à compression d’impulsion devrait avoir une résolution de hauteur de 1 mètre.
