Les Principes du Radar

Duplexeur monopulsé

Figure 1 : Jonctions du guide d’onde reliant les cornets d’une antenne monopulsé

Figure 3 : Trois T magique en série…

Figure 2 : T magique
 

Figure 4 : ... et une jonction en T de type E.

Duplexeur monopulsé

Un radar de poursuite utilise souvent une antenne monopulsée qui comporte quatre cornets d’alimentation identiques groupés en une grappe. L’énergie totale reçue par un cornet en particulier varie avec la position de la cible par rapport à l’angle de site et l’azimut du faisceau radar. Pour conduire le signal des cornets vers le récepteur, on utilise quatre jonctions de guide d’onde qui aboutissent dans le duplexeur.

La portée du radar dans un système monopulsé dépend de la somme (Σ) des signaux reçus par le quatre cornets. La différence entre les signaux venant des quatre cornets, à cause de l’azimut (Δ_Az) et de l’élévation (Δ_Él) de la cible par rapport à l’axe de l’antenne, permet d’auto-corriger la direction de cette dernière pour qu’elle suive la cible.

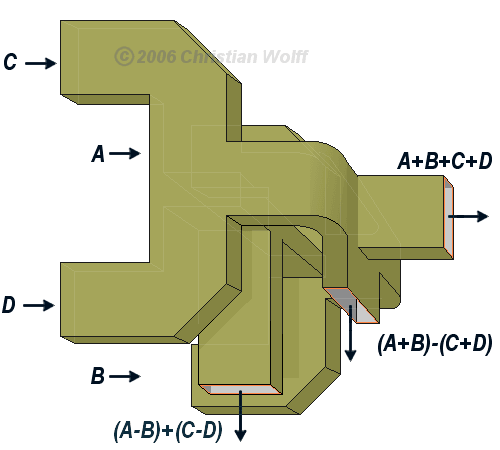
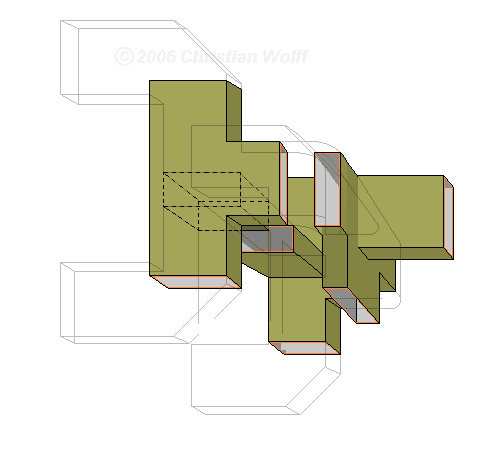
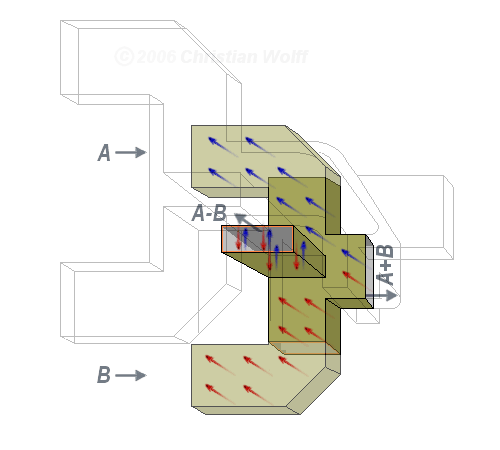
Le diagramme de la figure 1 montre le parcours de l’onde venant de chacun des cornets (A, B, C et D) vers les jonctions. Dans ce montage, on retrouve au total trois jonctions magiques en T qui peuvent donner les signaux:

1. A-B et A+B;
2. C-D et C+D
3. Δ_Él = (A+B)-(C+D) et Σ = A+B+C+D

Figure 5: Quadruple subdivided horn, in the common flange are continued four separate waveguides.

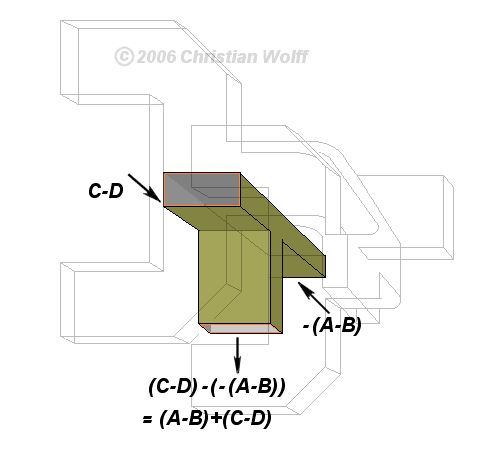
Puis une jonction en T de type E pour obtenir Δ_Az = (A-B)+(C-D).

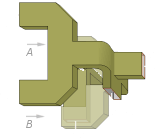
En général, le duplexeur est conçu pour laisser passer une onde polarisée horizontalement. La figure 2 montre la variation de l’axe des champs électrique lors du passage dans l’une des jonctions en T magique reliant les cornets A et B. La jonction et les coudes permettent d’obtenir la somme et la différence des signaux venant de ces deux cornets.

Si les deux ondes entrant A et B sont de même amplitude et polarité, en traversant la jonction en T type E du T magique, elles s’annuleront complètement et le signal de sortie de ce joint sera nul. Par contre, si elles sont d’intensité différente mais de même polarité, la sortie de la jonction sera la différence des deux signaux. La différence d’azimut (ΔAz_Az) entre les cornets de droite et de gauche sera le résultat la sortie de type E combinant les sorties de type H de droite et de gauche: (A+B)-(C+D).