Calcul de la position avec un radar bistatique
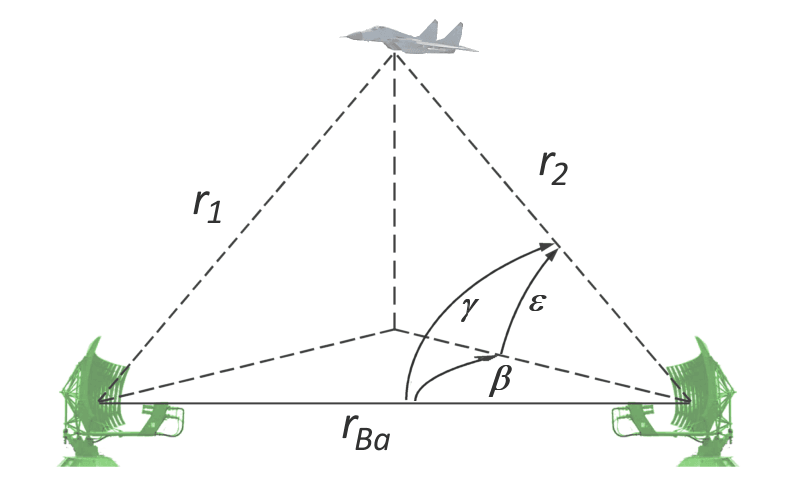
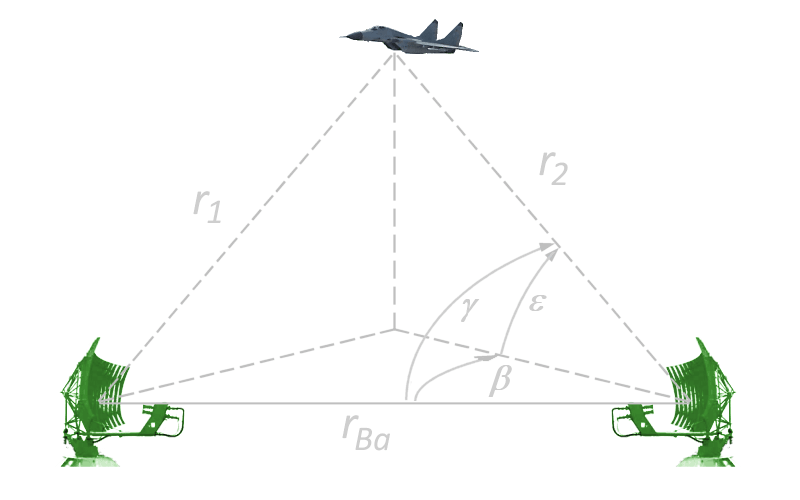
Figure 1 : Détermination de la position avec un radar bistatique
L'impulsion transmise par le radar primaire fait un aller-retour vers ce dernier (2 fois R1). Elle atteint également le récepteur secondaire après un trajet de rΣ = r1 + r2. La position de la cible avec trajet rΣ ne peut se trouver que sur l’ellipsoïde de rotation dont le radar primaire et l’antenne secondaire sont les deux foyers. L’angle latéral β entre la cible et la ligne joignant les deux radars (rBa) et l'angle d'élévation ε sont données par la position notés par le radar primaire.
rΣ est déterminé précisément par la mesure du temps de la réception de l’écho de retour par le radar primaire et la distance connue rBa. La distance entre la cible et l'antenne du récepteur (r2) peut être déterminée en utilisant la règle du cosinus et la distance totale mesurée rΣ. Cela nous donne deux équations:
| r12 = r22 + rBa2 - 2r2 · rBa · cos γ | |
| r1 + r2 = rΣ | (1) |
Ce système d'équations à deux inconnues peut être transformé ainsi:
| r2 = | rΣ2 - rBa2 | (2) |
| 2rΣ (1 - cos γ) |
L'angle γ est déterminé à partir des angles mesurés β et ε basé sur la relation entre ces trois angles:
| γ = arcos( cos β · cos ε) | (3) |
Cas limites
Un radar bistatique donne des résultats différents de celui du radar monostatique si la distance entre l’émetteur et le récepteur et celle à la cible se retrouve entre certaines limites. En général, plus β est près de 45 degrés, plus les résultats seront différents. Il existe deux cas où le concept bistatique peut encore être utilisé mais devient limite:
- Lorsque la cible est assez éloignée pour que R1 soit beaucoup plus grand que RBa,
on se retrouve dans la situation d’un radar monostatique:
- β tend vers 90 degrés;
- γ ≅ ε selon l’équation 3 ;
- R2 ≅ R1 selon l’équation 2 ;
- La vitesse radiale de la cible est la même pour les deux antennes.
- Lorsque la cible passe entre l’émetteur et le récepteur, on est dans la situation d’un radar barrière:
- β tend vers 0 ;
- γ = ε = 0 ;
- R1 et R2 sont indéterminés selon l’équation 2 ;
- La vitesse radiale est nulle car la cible passe tangentiellement.