Intégration des impulsions
L’intégration d’impulsions est une technique qui améliore la probabilité de détection des cibles en utilisant plusieurs périodes d'impulsions successives. Ceci est réalisé en incluant dans le traitement de signal reçu, un processeur supplémentaire qui fait une somme des signaux d'écho de ces d'impulsions. Selon le point d’insertion dans le circuit de l’intégrateur, il donne :
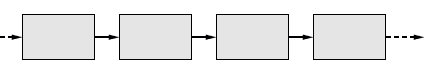
adapté
(Amplification FI))
cohérent
d’amplitude
l’appareil
non
détection
Figure 1 : Position dans un intégrateur cohérent.

adapté
(Amplification FI)
cohérent
d’amplitude
l’appareil
non
détection
Figure 1 : Position dans un intégrateur cohérent.
- une intégration cohérente ;
- une intégration incohérente.
Intégration cohérente
La figure montre un intégrateur mis entre le filtre adapté et le détecteur d’amplitudes. À cette position, il accumule les valeurs à chaque balayage pour des échantillons également espacés selon la résolution en portée du radar. Comme, l’échantillonnage contient toute l’information d’intensité et de phase des impulsions, il est dit cohérent.
L’intégrateur accumule ainsi jusqu’à N impulsions revenant du même endroit. Une fois qu’il à atteint N impulsions, les impulsions suivantes éliminent les plus anciennes dans la liste. L’intégrateur peut donc calculer la moyenne mobile à chaque distance de résolution et la comparer au seuil de réflectivité pour ces points.
Par exemple, avec un radar ayant une résolution en portée de 150 mètres, le processeur radar fournit 75 000 m/150 m échantillons, soit 500 par impulsion par balayage d’un azimut. L’intégrateur ajoute à chaque balayage les données provenant de ces 500 points dans 500 mémoires jusqu’à ce qu’il y ait N (1 à N) valeurs par mémoire et calcule la moyenne. Ensuite, pour chaque balayage supplémentaire en un point donné, N1 est éliminé pendant que les autres valeurs descendent d’un échelon dans la mémoire et que la nouvelle valeur pour ce point est mise en position N.
Dans un processeur analogue, l’accumulation et la somme se sont à l’aide de filtres. Dans les processeurs numériques, le tout est accompli en transformant le signal à l’aide d’une transformée de Fourier rapide.
Le bruit dans chaque impulsion suit une probabilité gaussienne et centrée sur zéro, les échantillons étant non corrélés. Ce bruit a donc les mêmes propriétés statistiques que celui du signal sortant du filtre adapté d’un amplificateur de fréquence intermédiaire (FI). En prenant pour acquis que l’intensité des signaux entrant dans l’intégrateur cohérent est assez constant d’une impulsion à l’autre, ceci correspond aux cas de cibles de Swerling 1, 3 ou 5. Chaque valeur correspond à une densité de probabilité pour un type de cible particulier et la somme des signaux, tel que décrit antérieurement, donne un rapport signal sur bruit (S/N) de N fois le rapport tiré de l’équation du radar pour la portée correspondante.
L’intégration cohérente n’offre aucun bénéfice pour les cas de cibles très fluctuantes des types Swerling 2 et 4, car les signaux provenant de ces types de cibles se comporte comme du bruit.
Intégration incohérente
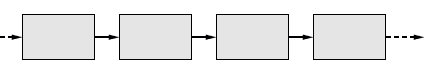
adapté
(Amplification FI)
d’amplitude
incohérent
l’appareil
non
détection
Figure 2 : Emplacement de l’intégrateur non cohérent.

adapté
(Amplification FI)
d’amplitude
incohérent
l’appareil
non
détection
Figure 2 : Emplacement de l’intégrateur non cohérent.
En plaçant l’intégrateur après le détecteur d’amplitude et de phase du signal, comme dans la figure 2, cette dernière est perdue et le signal n’analyse seulement que l’amplitude qui varie d’un écho à l’autre sans corrélation. C’est pourquoi cette intégration est dite incohérente.
L’intégrateur fonctionne de la même façon que celui cohérent. Dans les radars plus anciens, l’intégration utilisait la persistance de luminosité de l’écran d’affichage, l’opérateur pouvant percevoir les variations d’intensité des échos. Plus tard, on utilisa un détecteur dit m-de-n qui se servait d’un circuit électronique analogique déclarant un écho comme une cible si m échantillons de n étaient plus intenses qu’un seuil déterminé.
Un troisième type utilise un sommateur, une unité fonctionnelle dont la variable de sortie est égale à la somme, ou à une somme pondérée, des variables d'entrée. Il s’agit en général d’un filtre passe-bas dans les radars analogiques et d’un compteur numérique dédié dans les radars plus récents (similaires à ceux des intégrateurs cohérents).
