Transformée de Fourier rapide
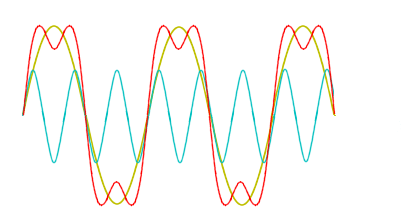
Figure 1 : Sinus de mode primaire (ambre) et sa troisième harmonique (cyan), dont la somme des amplitudes donne une onde s’approchant d’une onde carrée (rouge) dans le domaine temporel.
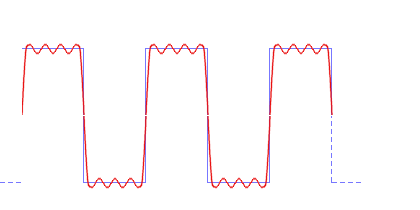
Figure 2 : En ajoutant la cinquième harmonique, le résultat est presque celui d’un onde carrée.
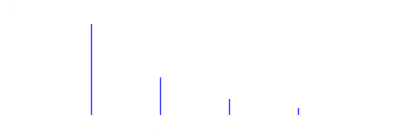
Figure 3 : Représentation des amplitudes relatives des différentes harmoniques (domaine fréquentiel) pour arriver à l’onde carrée.
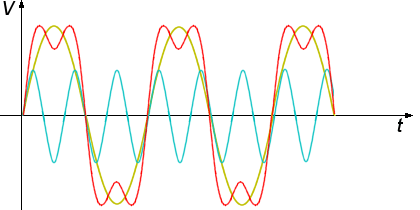
Figure 1 : Sinus de mode primaire (ambre) et sa troisième harmonique (cyan), dont la somme des amplitudes donne une onde s’approchant d’une onde carrée (rouge) dans le domaine temporel.
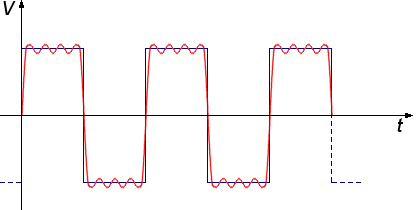
Figure 2 : En ajoutant la cinquième harmonique, le résultat est presque celui d’un onde carrée.
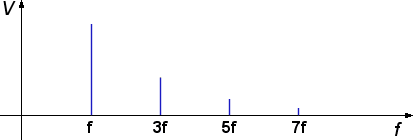
Figure 3 : Représentation des amplitudes relatives des différentes harmoniques (domaine fréquentiel) pour arriver à l’onde carrée.

Figure 1 : Sinus de mode primaire (ambre) et sa troisième harmonique (cyan), dont la somme des amplitudes donne une onde s’approchant d’une onde carrée (rouge) dans le domaine temporel.

Figure 2 : En ajoutant la cinquième harmonique, le résultat est presque celui d’un onde carrée.

Figure 3 : Représentation des amplitudes relatives des différentes harmoniques (domaine fréquentiel) pour arriver à l’onde carrée.
Transformée de Fourier rapide
La transformée de Fourier est l’intégrale du développement en série d’ondes harmoniques d’une onde complexe. Le principe a été émis par le mathématicien français Jean-Baptiste Joseph Fourier en 1822 dans son livre Théorie analytique de la chaleur. Le signal retourné par une cible est une telle onde dont l’amplitude et la phase sont reçues par le circuit du récepteur.
Dans la figure 1, on peut voir deux ondes dont la seconde (cyan) est de fréquence triple de la première (ambre). La somme de ces ondes donne une onde qui s’approche d’une onde carrée (rouge) mais avec des fluctuations. Dans la figure 2, une onde avec une fréquence cinq fois celle de la première est ajoutée et l’onde finale devient plus carrée. Tout signal retourné au radar peut être ainsi analysé en une série de sinus et de cosinus ayant des fréquences, phases et amplitudes différentes. La figure 3 montre les amplitudes que doivent avoir chacune des harmoniques pour donner une onde de plus en plus carrée.
Le traitement Doppler par paires d’impulsions est fondé sur le calcul du spectre de fréquences de ce signal, obtenues par une transformée de Fourier des données du domaine temporel. Cette transformation est donc devenue un élément fondamental de traitement du signal radar. En principe, il existe une solution analytique à tout signal mais en pratique cette transformation est difficile dans le cas d’une onde quelconque. C’est pourquoi, l’analyse est faite à partir d’un échantillonnage temporel des amplitudes et phases du signal. Le traitement devient alors une somme des harmoniques, soit une transformée de Fourier discrète (TFD).
Cette conversion prend beaucoup de temps informatique et un algorithme informatique plus récent, la transformée de Fourier rapide (TFR), a permis de résoudre le problème en temps réel. La vitesse de l’analyse dépend:
- Du choix de l’algorithme approprié au type de signal;
- De l’utilisation d’additions dans le programme plutôt que de multiplications, les secondes prenant plus de temps machine;
- Les résultants des premières harmoniques peuvent être utilisés comme première approximation.
Comme la TFR extrait les composantes de fréquences du signal, les données à emmagasiner en mémoire sont réduites. Le signal radar transformé peut donc être gardé pour usage futur, par exemple pour reconnaître une cible car son signal est unique, comme une empreinte digitale. Il est aussi possible de faire la transformée inverse pour obtenir le signal échantillonné original.
Pour plus d’informations :
Srishti D. Chatterji Cours d'analyse, Presses Polytechniques et Universitaires Romandes, 1998 (ISBN 978-2880743468)
Matteo Frigo and Steven G. Johnson: FFTW,
http://www.fftw.org/ :
Une implémentation libre (GPL) de la transformée de Fourier rapide (bibliothèque C) pour des données de taille et de dimensions arbitraires.
« The Design and Implementation of FFTW3 »,
Proceedings of the IEEE 93 (2), 216–231 (2005).
