Lissage de trajectoire
antérieures
(balayage n-1)
de la prochaine détection
Figure 1 : Lissage de la trajectoire
(balayage n-1)
de la prochaine détection
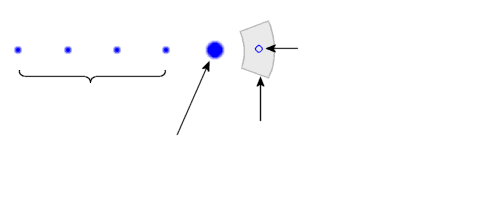
Figure 1 : Lissage de la trajectoire

(balayage n-1)
de la prochaine détection
Figure 1 : Lissage de la trajectoire
Lissage de trajectoire
Le rôle du lissage de la trajectoire est de prendre les données de la dernière détection d’une cible (position, vitesse, direction de déplacement et possiblement son accélération) et de faire une meilleure prédiction de celles-ci au balayage suivant. Ce processus permet également de corriger les mouvements aléatoires causés par l’analyse primaire de la trajectoire faite à partir d’une histoire limitée. Le lissage se fait en utilisant la plus récente trajectoire prévue et la combine avec les données disponibles sur une plus longue période.
Il existe une grande variété d’algorithmes, plus ou moins complexes, pour arriver à faire ce lissage, qui sont utilisés comme autant de filtres. Tous ces filtres fonctionnent en deux étapes :
- Prédiction ;
- Correction.
La position de la cible pour au moins les deux derniers balayages, mais en général plus, est noté. Ensuite, les coefficients de l’algorithme sont ajustés pour donner une trajectoire qui passe au voisinage de ces points tout en tenant compte de la vitesse et de l’accélération de la cible, tout en minimisant l’écart entre la position réelle et celle de la trajectoire calculée. De là, une position future est obtenue.
Algorithme Alpha-Beta
Une des premières approches à ce problème est celui de l’algorithme Alpha-Beta. Il s’agit d’une forme simplifiée de l’observateur pour l’estimation, le lissage et les applications de contrôle. Il est intimement relié aux filtres de Kalman et à l’extrapolation linéaire que les observateurs utilisent dans la théorie du contrôle. Son avantage principal est sa simplicité, l’algorithme utilise l’hypothèse d’une erreur gaussienne et d’une vitesse constante où la cible ne change pas de cap trop brusquement.
Filtre de Kalman
Le filtre de Kalman est une méthode mathématique développée par l’ingénieur en électricité et professeur d’origine américano-hongroise Rudolf Kalman. Il s’agit d’un filtre à réponse impulsionnelle infinie qui estime les états d'un système dynamique à partir d'une série de mesures incomplètes ou bruitées. Il est devenu l’algorithme principal pour le traitement des trajectoires dans les systèmes radar modernes.
Le filtre de Kalman est un estimateur récursif. Cela signifie que pour estimer l'état courant, seuls l'état précédent (positions, direction, et possiblement accélération, au balayage n-1) et les mesures actuelles (balayage n) sont nécessaires. L'historique des observations et des estimations n'est ainsi pas requis.
Le filtre de Kalman a deux phases distinctes: Prédiction et Mise à jour. La phase de prédiction utilise l'état estimé de l'instant précédent pour produire une estimation de l'état courant. Dans l'étape de mise à jour, les observations de l'instant courant sont utilisées pour corriger l'état prédit dans le but d'obtenir une estimation plus précise. Dans cette seconde étape, l’algorithme ajuste les valeurs d’erreurs associées aux positions historiques.
Une hypothèse clé de l’algorithme est que les équations de mesure (c’est-à-dire la relation entre les données radar et l’état de la cible) et les équations d’état (c’est-à-dire les équations prédisant l’état future basé sur l’état présent) sont linéaires de la forme y = A·x, avec A une constante, et non de la forme y = f(x).
Le filtre de Kalman prend pour acquis que toutes les erreurs (mesure, prédiction de déplacement, état) sont des gaussienne centrées à zéro. Cela implique que toutes les sources d’erreur peuvent être incluses dans une matrice de covariance. Le filtre de Kalman utilise ces matrices de covariance pour estimer la pondération des différents facteurs de l’équation et les ajustent dans le temps aux différentes observations et prédictions.
Si la cible se comporte très près de ce que le modèle le prédit, le filtre de Kalman a tendance à devenir trop « confiant » dans ses prédictions et commence à rejeter de l’analyse les nouvelles mesures réelles du radar si elles s’en écartent. Pour éviter cela, le poids des nouvelles observations dans les matrices de covariante est légèrement rehaussé par rapport à la prédiction.
