Track Smoothing
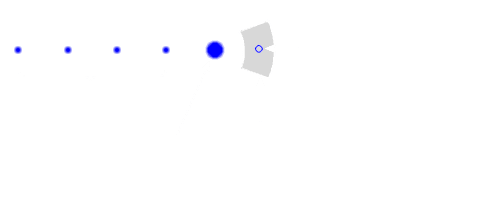
(scan n-1)
of the next
plot detection
Figure 1: Process of track smoothing
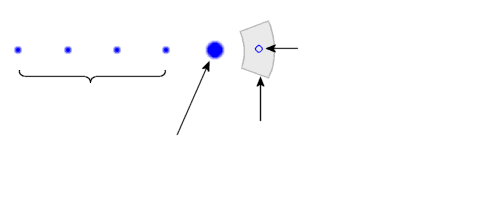
(scan n-1)
of the next plot detection
Figure 1: Process of track smoothing

(scan n-1)
of the next plot detection
Figure 1: Process of track smoothing
Track Smoothing
The role of the track-smoothing function is to take the current known state (i.e. position, heading, speed and possibly acceleration) of the target and predict the new state of the target at the time of the most recent radar measurement. It is a computing step to improve the estimate of the tracks position as well as to revise the errors in the former prediction. The latest track prediction is combined with the associated plot to provide a new, improved estimate of the next target state. There are a wide variety of algorithms, of differing complexity and computational load that can be used for this process. These algorithms are realized in special filters.
All of these filters work in two steps:
- prediction, and
- correction.
The observed position of the target is recorded for the last two or more scans. Then, the smoothed parameters (often called innovations) are computed for position, velocity and acceleration. Using these values, the predictions for position and velocity are computed.
Alpha-Beta Tracker
An early tracking approach is the so-called Alpha-beta tracker. It is a simplified form of observer for estimation, data smoothing and control applications. It is closely related to Kalman filters and to linear state observers used in control theory. Its principal advantage is that it does not require a detailed system model. This tracker assumed fixed Gaussian errors and a constant-speed, non-maneuvering target model to update tracks.
Kalman Filter
The Kalman filter is a mathematical method named after Rudolf Kalman, an Hungarian-American electrical engineer, mathematical system theorist, and college professor. The purpose of the Kalman filter is to use measurements that are observed over time that contain noise or random variations and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated values. It is the central algorithm to the majority of all modern radar tracking systems.
The Kalman filter is a recursive estimator. This means that only the estimated state from the previous time step and the current known state of the target (i.e. position, heading, speed and possibly acceleration from scan n-1) are needed to compute the estimate and predict the new state of the target at the time of the most recent radar measurement (scan n).
In making this prediction, it also updates its estimate of its own uncertainty (i.e. errors) in this prediction. It then forms a weighted average of this prediction of state and the latest measurement of state, taking account of the known measurement errors of the radar and its own uncertainty in the target motion models. Finally, it updates its estimate of its uncertainty of the state estimate. A key assumption in the mathematics of the Kalman filter is that measurement equations (i.e. the relationship between the radar measurements and the target state) and the state equations (i.e. the equations for predicting a future state based on the current state) are linear – i.e. can be expressed in the form y = A·x (where A is a constant), rather than y = f(x).
The Kalman filter assumes that the measurement errors of the radar, and the errors in its target motion model, and the errors in its state estimate are all zero-mean Gaussian distributed. This means that all of these sources of errors can be represented by a covariance matrix. The mathematics of the Kalman filter is therefore concerned with propagating these covariance matrices and using them to form the weighted sum of prediction and measurement.
In situations where the target motion conforms well to the underlying model, there is a tendency of the Kalman filter to become “over confident” of its own predictions and to start to ignore the radar measurements. If the target then maneuvers, the filter will fail to follow the maneuver. It is therefore common practice when implementing the filter to arbitrarily increase the magnitude of the state estimate covariance matrix slightly at each update to prevent this.
