Blind Speed
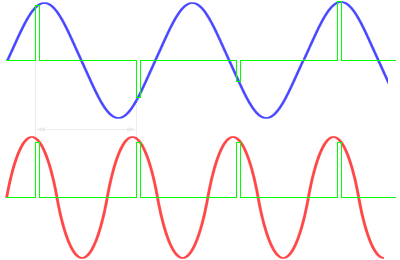
Figure 1: Blind speed in connexion with the Doppler-shift
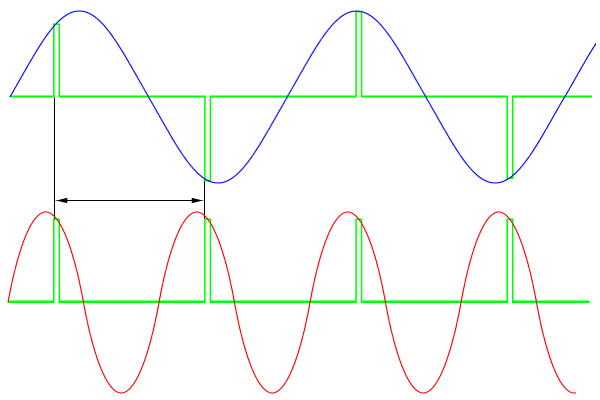
Figure 1: Blind speed in connexion with the Doppler-shift
Blind Speed
At the comparison of the echoes between two or more pulse periods the fall can appear, that the airplane flies with exactly this one radial speed, some a phase shifting of correct 360° causes. In accordance with the periodicity of the sine function this fall can appear even at all integral multiples of ±n · 360°. The value of phase shifting is zero in these falls too. Well, the target isn't recognized as a moving target therefore. It flies with a so-called blind speed and the MTI system won't report it like a ground clutter.
The blind speed is dependent on the transmitted frequency and on the pulse repetition frequency of the radar unit.
| vblind = | λ | where: |
vblind = one of the blind speeds λ = wavelength of the transmitted pulse Ts = pulse repetition time (PRT) |
(1) |
| 2·Ts |
With reference to the lower diagram on the figure 1:
If the Doppler frequency produced by a moving target is exactly the same as the PRF
(fD = PRF) then “sampling” occurs at the same point on each Doppler cycle.
As far as the signal processor is concerned, it is as if the target were stationary.
The same effect occurs if fD is an integer multiple of PRF.
Hence targets with certain radial velocities tend to be invisible to an MTI pulse radar.
The blind speed is a radial speed of the airplane at which the phase shifting of the echo-signal has the value ±n · 360° between two pulse periods. With blind speeds moving targets are suppressed by a MTI system like ground clutters.
Example given:
A radar unit works with the tx-frequency of 2.8 GHz and a puls repetition time of 1.5 ms.
Under these conditions the first blind speed has got the value:
| vblind = | λ | = | c0 | = | 3·108 | = 35,72 m/s | c0 = speed of light | (2) |
| 2·Ts | 2·f·Ts | 2·2,8·109·1,5·10-3 |
This speed of converted about 130 km/h and all integral multiples of this also well cause that the target isn't visible in the range of the effectiveness of the MTI system.
Due to the periodicity of a measured Doppler frequency is only in the period from zero to the first maximum of the sine wave in Figure 1 (representing the Doppler frequency) unambiguously assigned to a velocity. The doppler frequency must be lower than the pulse repetition frequency. This ambiguity in measurements of velocity is called Doppler Dilemma.
Simple measures against the appearance of blind speeds are:
- Using of the coherence channel only if it is necessary
This demand also arises that the amplitude channel („Normal Video”) has a better maximum range than the „Coho-channel”. - constantly changing of the TX- frequency (Frequency-Diversity)
It is demanded a sufficiently large frequency spacing. - constantly changing of the pulse repetition time (Staggered PRT)
Most effective resource: no airplane can change its speed so fast and synchronous still to this!
However, all these measures are part of the standards of air-surveillance radar sets already.
