Système de coordonnées
Selon les besoins, il conviendra de tracer des diagrammes et des graphiques dans un système de coordonnées plutôt qu’un autre. Les plus courantes sont les coordonnées cartésiennes, polaires, cylindriques et sphériques.
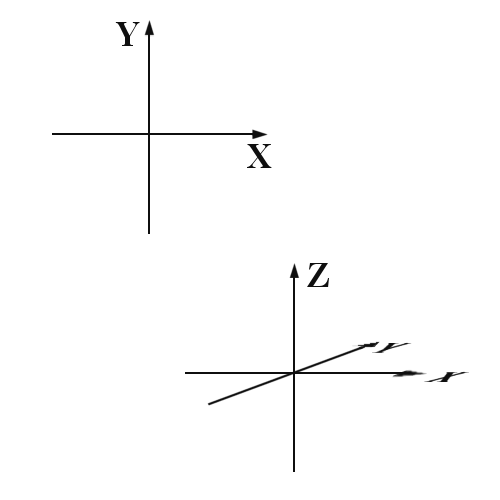
Figure 1 : Dimensions
dimensions
Figure 1 : Dimensions
Cartésiennes
Le système cartésien est le plus courant. Les axes y sont à angles droits les uns des autres. Il permet de déterminer la position d'un point sur une droite, dans un plan ou dans l'espace à condition d'avoir défini un repère cartésien. Ce système est conçu pour afficher une fonction y= f(x) en deux dimensions ou une fonction z = f(x, y) en trois dimensions. Il peut également servir à tracer un vecteur ayant des composantes x, y et z.
Les axes d’un système cartésien ne sont pas nécessairement linéaires et peuvent également suivre une progression différente selon l’axe. Les axes ne sont pas nécessairement non plus des données de distance. Par exemple dans la figure 2, le diagramme d’émission d’une antenne a été tracé. L’axe des X représente l’angle par rapport à la direction du faisceau principal et il est linaire. Par contre l’axe Y représente l’intensité du signal et suit une progression logarithmique (dB) où chaque ligne graduation représente dix fois la valeur de la précédente.
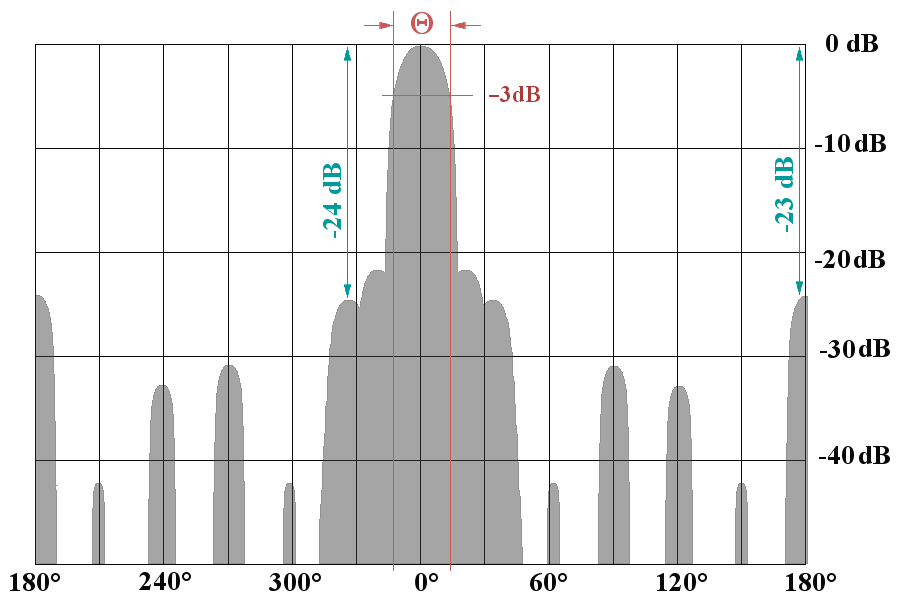
Figure 2 : Diagramme d’émission d’une antenne en coordonnées cartésiennes.
Figure 2 : Diagramme d’émission d’une antenne en coordonnées cartésiennes.
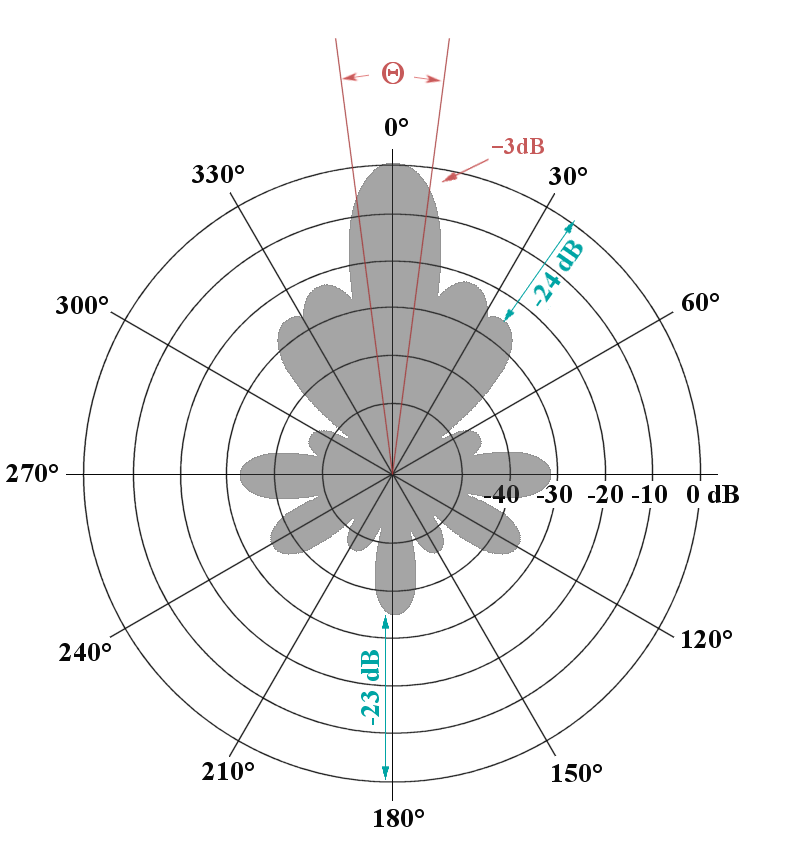
Figure 3 : Diagramme d’émission d’antenne en coordonnées polaires.
Figure 3 : Diagramme d’émission d’antenne en coordonnées polaires.
Polaires
Lorsque les données sont à trois dimensions, le diagramme polaire peut devenir un diagramme cylindrique ou sphérique. Par exemple, pour représenter le diagramme d’émission d’une antenne en trois dimensions, où la troisième dimension est l’angle d’élévation, on utilisera les coordonnées sphériques (ρ, θ et φ). Par contre, si la troisième dimension est la hauteur (z), ce seront les coordonnées cylindriques qui seront utilisées.
