Décalage Doppler du fouillis radar
déplacement
du porteur
synthétique L
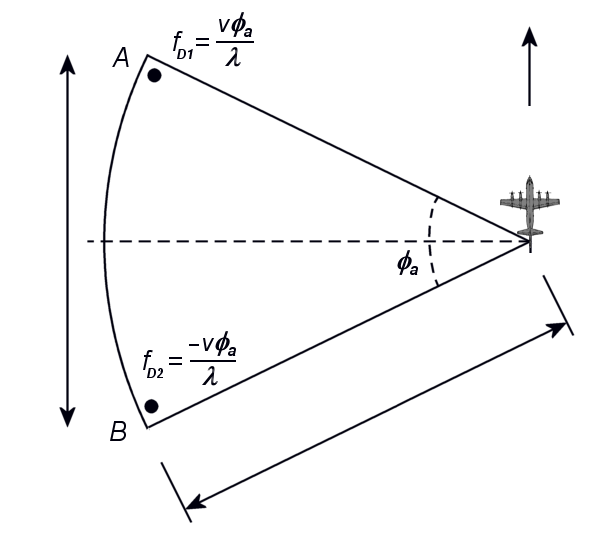
Figure 1 : Une cible stationnaire dans un faisceau radar en mouvement
déplacement
du porteur
synthétique L
Figure 1 : Une cible stationnaire dans un faisceau radar en mouvement
Décalage Doppler du fouillis radar
Dans la figure 1, un RSO sonde deux cibles ponctuelles stationnaires en A et B se trouvant sur les bords du faisceau radar. À cause du déplacement du porteur du radar au temps de l’image, le point B s’éloigne et le point A s’approche radialement du radar. Le décalage Doppler (fD) est relié à la vitesse radiale vers le radar qui sera maximale (fmax) dans la direction de déplacement du porteur du radar (θ=0°) et nul dans la direction de visée perpendiculaire au trajet du porteur (θ=90°):
| fD = fmax · cosθ | (1) |
La variation de fD est sa dérivée par rapport à θ:
| dfD = -fmax · sinθ dθ | (2) |
Comme le radar pointe vers l’angle θ=90°, le sinus est égal à 1 et:
| dfD = -fmax dθ | (3) |
On voit aussi dans l’équation et la figure 2 que si la largeur du faisceau est fixe, le décalage (dfD) entre les deux bords du faisceau (dθ) sera une constance, quel que soit la distance, c’est ce qu’on appelle la bande passante Doppler du radar. Toute cible stationnaire passant dans un faisceau de RSO aura un décalage qui se situera à l’intérieur de cette bande.
La variation temporelle s’exprime par:
| fD1 - fD2 = | = - fmax | dθa | (4) |
| dt | dt |
Pour un radar ayant une largeur de faisceau mince, le dθ⁄dt est à peu près linéaire. Donc, la variation du décalage Doppler entre A et B avec le temps (dfD⁄dt) dépendra de la distance au radar, plus les points sont distants du radar (R) plus le changement angulaire sera lent car dθ représente une plus longue distance (Rdθ). La distance R pour chaque cible peut ainsi être calculée avec la variation temporelle de fD pour cette cible, indépendamment du temps de retour de l’écho. La position angulaire sera celle de la direction où le décalage est nul (fD = 0).
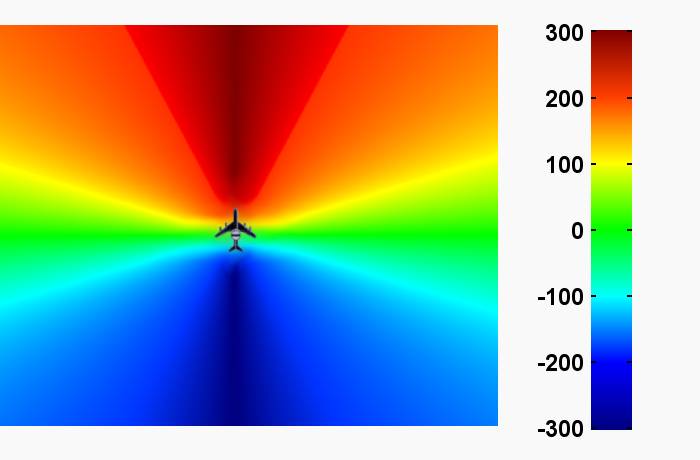
Figure 2 : Variation du décalage Doppler en Hz selon l’angle d’incidence au radar quand ce dernier point perpendiculairement à la trajectoire (exemple avec v = 100 m/s)
Figure 2 : Variation du décalage Doppler en Hz selon l’angle d’incidence au radar quand ce dernier point perpendiculairement à la trajectoire (exemple avec v = 100 m/s)
Cette variation est similaire à la réponse à un radar émettant une modulation de fréquence linéaire (radar « chirp ») pour donner une impulsion compressée de longueur R·φa. En utilisant les caractéristiques du radar, la variation du décalage Doppler de B à A pour un faisceau mince est donnée par:
| fD1 - fD2 = | 2v · φa | v = vitesse par rapport au sol du porteur-radar φa = largeur du faisceau (diminution de -3dB de l’intensité centrale) λ = longueur d’onde du radar. |
(5) |
| λ |
Le décalage Doppler doit être ensuite « normalisé », c’est-à-dire divisée par la fréquence de l’onde porteuse, pour traitement ultérieur.
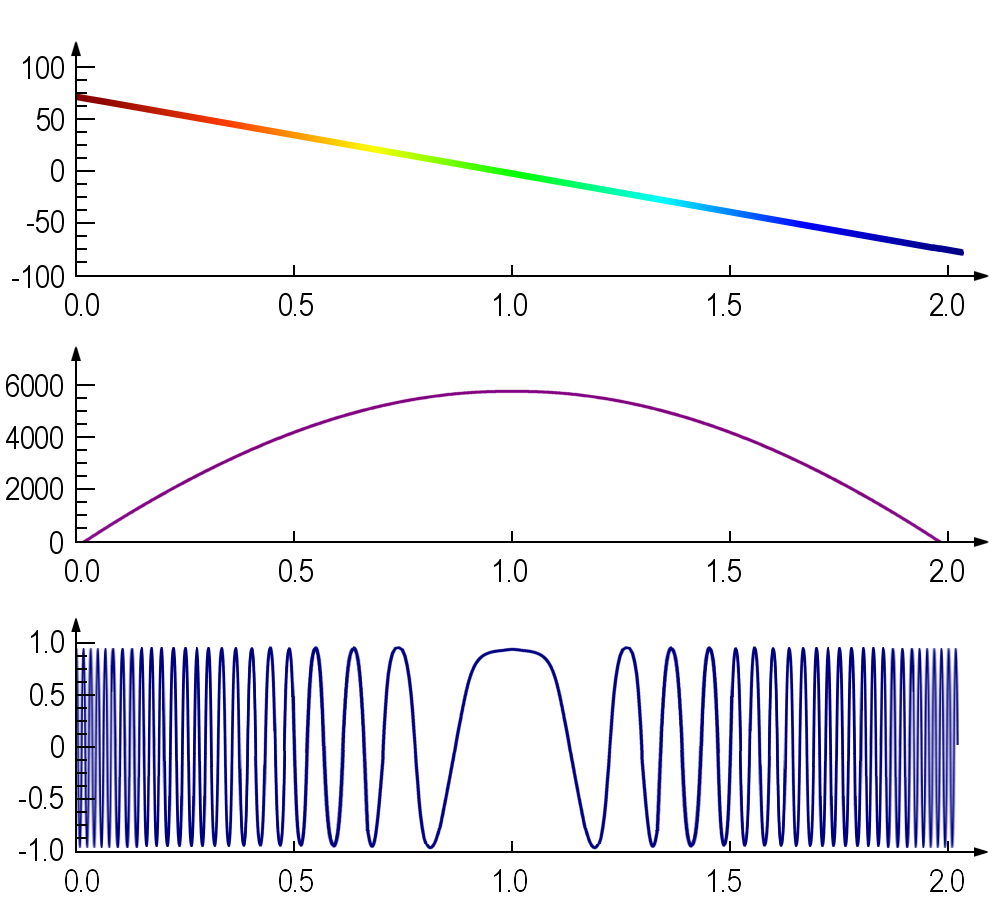
Figure 3 : Progression du décalage Doppler, de la phase et de l’amplitude d’un rétrodiffuseur ponctuel.
Figure 3 : Progression du décalage Doppler, de la phase et de l’amplitude d’un rétrodiffuseur ponctuel.
Cibles en mouvement avec un RSO
En principe, le traitement RSO se concentre sur l’historique de la phase des cibles. Le programme prend pour acquis que les rétrodiffusions dans la zone étudiée sont stationnaires durant la période de sondage. Chaque point est ainsi caractérisé par une série temporelle unique de sa phase que le programme utilise pour déterminer sa position.
Cependant, si la cible est en mouvement, sa phase va varier avec un biais. Selon la direction et la vitesse de ce mouvement, la phase brute peut résulter en un positionnement erroné dans le cas le plus simple (direction et vitesse constante), jusqu’à une répartition en nuage (variation de direction et de vitesse durant les différents sondages) de cette position ce qui rend la détection impossible. Par exemple, les cartes RSO océaniques montrent souvent les navires et leur vague d’étrave séparément.
Une façon de corriger ce bais est par une analyse espace-temps des caractéristiques du diffuseur qui permet de différencier les cibles fixes des cibles mobiles.
