Calcul de l'altitude de la cible

Figure 1 : Relation trigonométrique simple entre l’élévation et la hauteur.
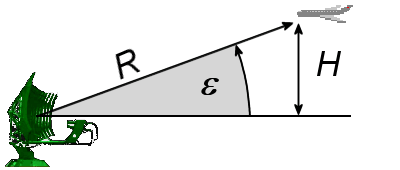
Figure 1 : Relation trigonométrique simple entre l’élévation et la hauteur.

Figure 1 : Relation trigonométrique simple entre l’élévation et la hauteur.
Calcul de l'altitude de la cible
La hauteur d'une cible par rapport à la surface du globe terrestre est appelée altitude. Dans les formules et schémas de cette page, elle sera désignée par la lettre H (comme Hauteur). L'altitude peut être calculée à partir des mesures de distance R et d'angle de site ε.
.fr.print.png)
.fr.png)
(1)
Nous insérons ces valeurs dans la formule:
(2)
Dans la réalité, l'altitude précise d'un avion en vol ne peut être calculée aussi simplement car lors de la propagation des ondes électromagnétiques, une réfraction se produit à chaque fois qu'elles atteignent une couche de l'atmosphère de différente densité, la surface de la terre est courbe. Ces deux facteurs sont compensés dans les systèmes radars qui calculent l'altitude grâce à l'utilisation d'une formule plus complète.
Le calcul de l'altitude de la cible n'est pas uniquement la simple résolution d'une équation trigonométrique appliquée au triangle. La rotondité de la terre doit également être prise en compte.
.print.png)
.png)
(3)
- R = distance de la cible en ligne droite
- ε = angle de site mesuré
- re = rayon moyen de la terre (environ 6370 km)
- (Cette formule n'est qu'approximative!)

Figure 2 : relation entre l'altitude et la hauteur à l'étude de la terre coude
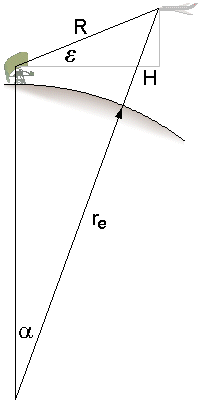
Figure 2 : relation entre l'altitude et la hauteur à l'étude de la terre coude

Figure 2 : relation entre l'altitude et la hauteur à l'étude de la terre coude
On peut déterminer l'équation à partir de la Figure 2. Un triangle est formé par les points: centre de la terre, position géographique du radar, et position de la cible (avion). Les cotés du triangle sont ceux qui sont repris dans la formule du cosinus et donc dans l'équation suivante:
(4)
En considérant que la terre est une sphère, l'arc de circonférence de la terre peut être calculé par le simple rapport entre la circonférence totale de la terre et l'angle α:
(5)
En pratique, cependant, la propagation des ondes électromagnétiques est soumise à la réfraction, c'est à dire que le faisceau d'ondes émis par le radar est un triangle dont les cotés sont courbés eux aussi, en fonction de:
- la longueur d'onde utilisée,
- la pression barométrique,
- la température de l'air
- le degré d'hygrométrie.
Pour tenir compte de la réfraction, le rayon dans la formule est changé pour le rayon de réfraction terrestre moyen (RÄ) égal à 4/3·re ≈ 8500 km et un terme est ajouté pour tenir compte des valeurs actuelles de température, d’humidité et de pression. A titre d'exemple, la formule suivante est utilisée pour déterminer l'altitude d'une cible par le radar d'altimétrie PRW–16
06.png) (6)
(6)
Avec comme termes:
- altitude sans prendre en compte le rayon de la terre;
- compensation du rayon de réfraction terrestre (environ 8 500 km);
- compensation de la réfraction dans l'atmosphère;
- influence de la température sur la réfraction.
