What is a waveguide?
Notions de base de la théorie des guides d'ondes

Figure 1 : Dimensions d’un guide d’ondes rectangulaire, ici une très courte section avec un raccord à piège pour des fréquences de 18,0 à 26,5 GHz.

Figure 1 : Dimensions d’un guide d’ondes rectangulaire, ici une très courte section avec un raccord à piège pour des fréquences de 18,0 à 26,5 GHz.
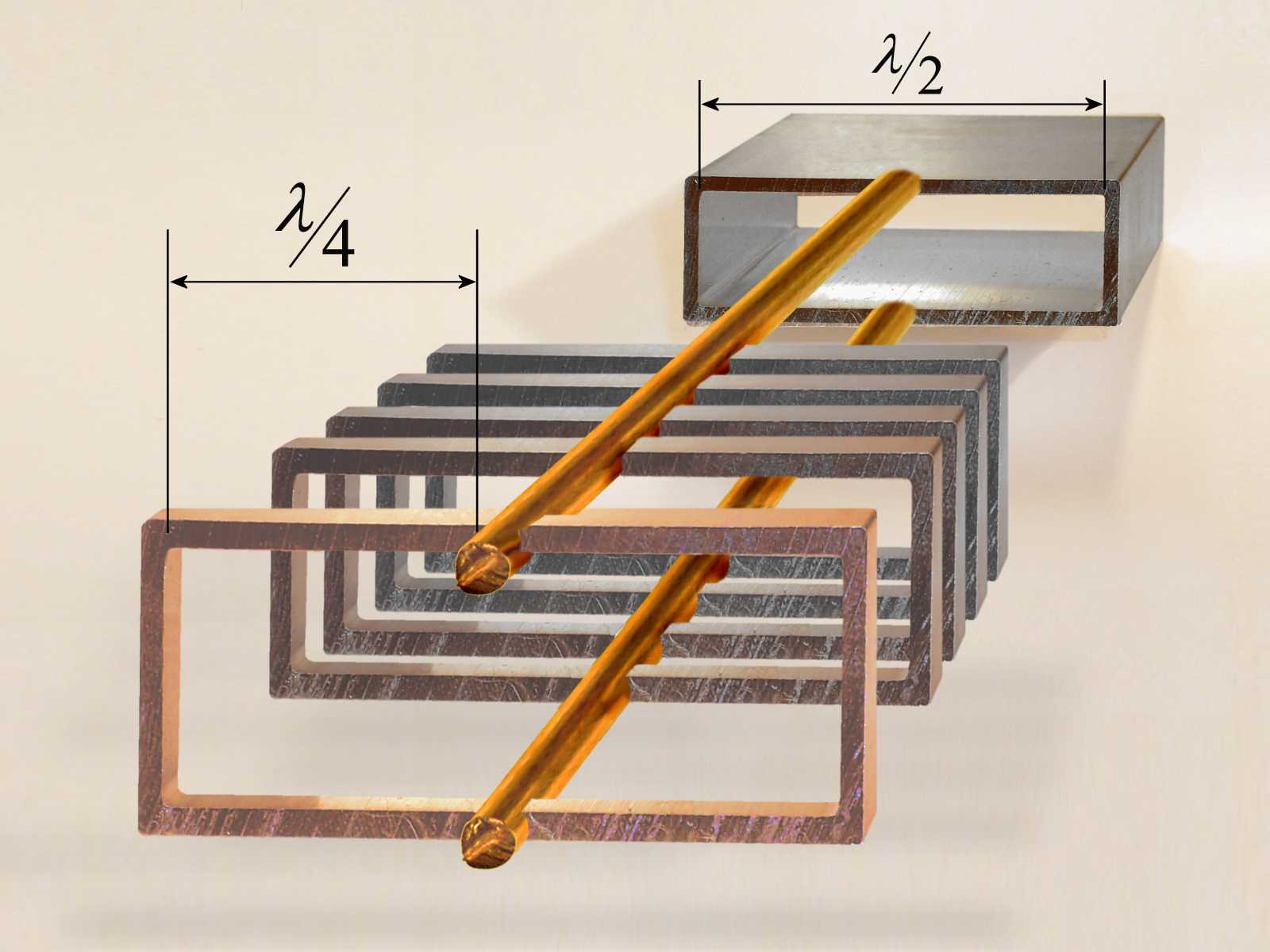
Figure 2 : Construire un guide d’onde en ajoutant des sections quart d’onde reliées par deux fils.
Notions de base de la théorie des guides d'ondes
Le guide d'ondes est une forme particulière de la ligne de transmission utilisée pour les applications micro-ondes. Il s’agit de tubes métalliques fait de matériaux de haute qualité (cuivre et laiton - partiellement argenté ou même plaqué or). Dans la technologie récente, ces guides sont composés de cuivre plaqué électriquement d’une mince couche de fibres de carbone.[1]
Un guide d'ondes peut avoir une section transversale rectangulaire, circulaire ou elliptique, la section rectangulaire étant la plus couramment utilisée pour les connexions relativement courtes. Les guides d’onde ont plusieurs avantages par rapport à la transmission par fils et lignes coaxiales. Le principal avantage est la minimisation de la perte lors de la transmission. Les champs électriques et magnétiques, qui sont utilisés pour le transport de l'énergie, sont égaux à zéro dans les surfaces métalliques. Par conséquent, ces champs sont confinés à l'espace interne du guide ce qui minimise les pertes. Ils sont de plus complètement blindés ce qui entraîne une bonne immunité des très faibles signaux transmis aux interférences externes.
Les guides d'ondes présentent des avantages théoriques considérables par rapport aux lignes coaxiales, mais en pratique ces avantages ne sont utilisés efficacement qu’à des fréquences supérieures à 1 GHz. En effet, les pertes dans les câbles coaxiaux sont provoquées par leur propre capacitance et inductance ainsi qu’à l'effet pelliculaire. Cette atténuation augmente significativement avec la fréquence de transmission et au-dessus de 36 GHz, les câbles coaxiaux sont rarement utilisables.
La résistance au claquage de ces câbles est aussi limitée par la faible distance entre les conducteurs intérieurs et extérieurs ce qui augmente les pertes. Ces inconvénients sont encore acceptables pour les signaux de faible puissance, mais à haute puissance elles conduisent à des pertes inacceptables.
Principe du guide d'ondes
Une ligne de transmission à deux fils ordinaire devrait être soutenue à intervalles réguliers par des isolateurs. À la jonction avec la ligne, les isolateurs doivent avoir une très haute impédance à la terre pour un fonctionnement correct. Un meilleur isolant à haute fréquence est une terminaison de résonance, à savoir une section quart d'onde appariée à la ligne de transmission et en court-circuit à une extrémité. Si l’adaptation est bonne, ce genre d'isolateurs va transformer le court-circuit de très haute impédance de la ligne de transmission à deux fils.
La figure 2 montre plusieurs moignons de résonance de chaque côté d'une ligne de transmission à deux fils. Lorsque des moignons sont ajoutés, chaque section est en contact avec l'autre, et un guide d'onde rectangulaire est formé. L'ancienne ligne de transmission à deux fils se trouve intégrée dans les parois de celui-ci. Ce guide a maintenant une largeur de λ /2.
On notera que les moignons de résonance sont des isolants à une seule fréquence. Cela limite grandement la largeur de bande et l'efficacité. Les signaux peuvent se propager dans le guide d'ondes seulement au-dessus d'une certaine fréquence. Celle-ci est fonction des dimensions du guide d'ondes, en particulier du mur «a». La propagation se produit seulement si la longueur d'onde à transférer est inférieure à la longueur d'onde dite de coupure (λcoupe).
La longueur d'onde de coupure d'un guide d'ondes rectangulaire est obtenue à partir de la formule :
| λcoupe = 2 · a | λcoupe = longueur d’onde de coupure [m] a = côté le plus grande du guide [m] (figure 1) |
En fait, les ondes de cette longueur ne peuvent pas passer efficacement dans le guide d'ondes. Ce dernier doit être d'environ 30% plus grand que cette demi-longueur d'onde afin de fonctionner efficacement ce qui rend l'utilisation de guides d'ondes à des fréquences inférieures à 1000 mégahertz graduellement moins pratique.
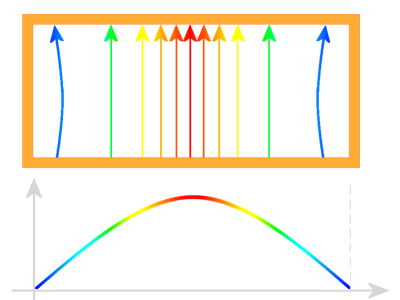
Figure 3 : Vu en coupe du champs électrique dans un guide d’ondes Mode TE10)
La section de guide de la figure 1 est faite à partir d’un tube de laiton rectangulaire extrudé de type WR42. WR signifie « guide d'onde rectangulaire », et le nombre désigné la dimension intérieure du côté large du guide d'ondes en centièmes de pouce :
- Le côté « a » est donc exactement 0,42 pouces, soit 0,42 x 25,4 mm = 10,67 mm de large ;
- La largeur de « b » est exactement la moitié de « a », soit 5,34 mm ;
- Sa fréquence de coupure minimale est 14,051 GHz et la transmission à faible atténuation commence seulement à une fréquence de 30% au-dessus de celle-ci ;
- Une fréquence de coupure supérieure est déterminée par l'état de la propagation d'un mauvais mode de propagation dont la fréquence de coupure inférieure est 28,102 GHz dans ce guide d'onde. La fréquence de coupure supérieure pour le mode de base est d'environ 5% plus faible ;
- La bande de fréquence correspondante pour ce type de guide d'onde est comprise entre 18,0 GHz et 26,5 GHz pour la transmission à faible pertes.[2]
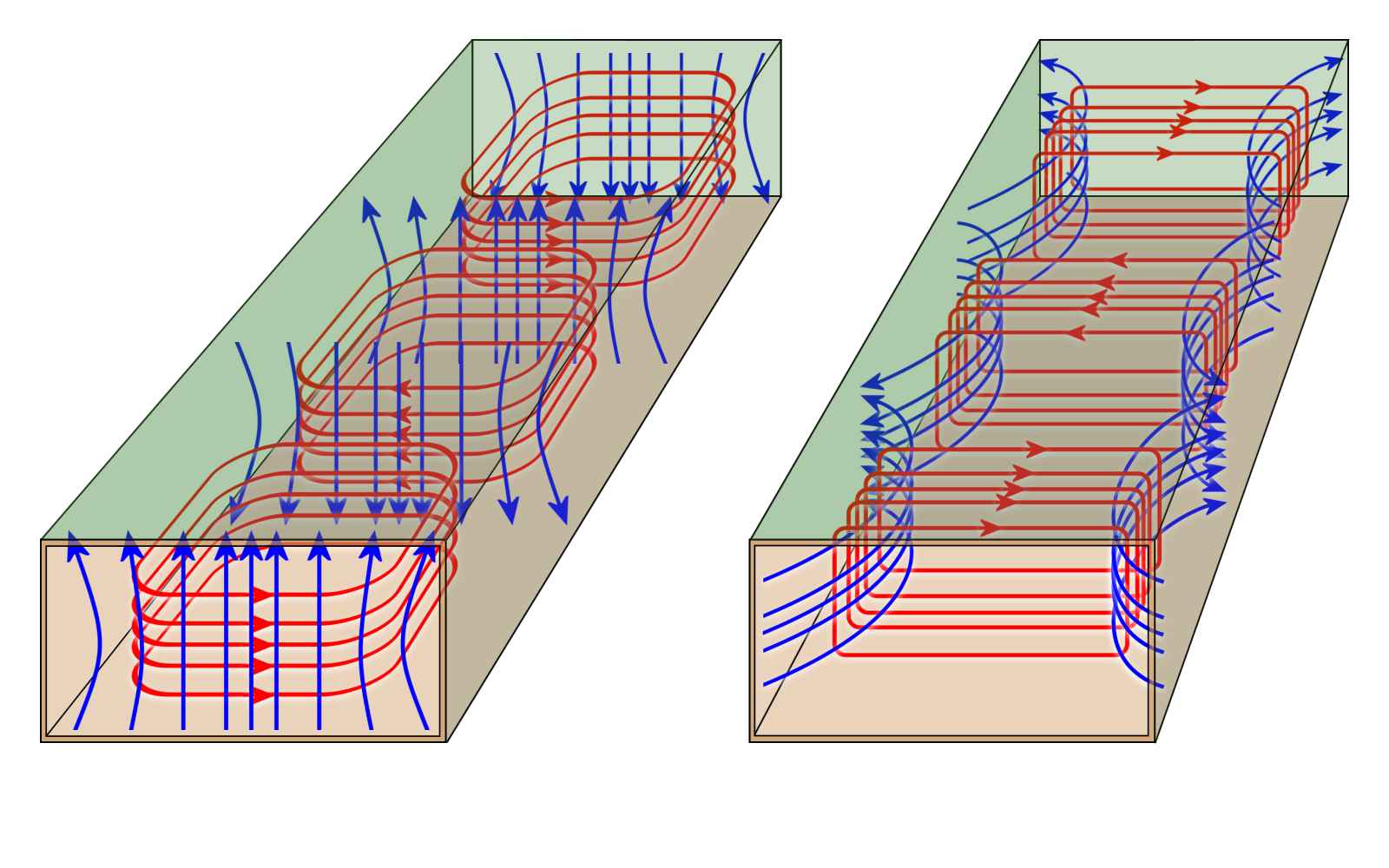
magnétique
Figure 3 : Description générale des modes de transmission dans un guide d’ondes
magnétique
Figure 4 : Description générale des modes de transmission dans un guide d’ondes
Propagation de l’onde électromagnétique dans un guide d’onde
Lorsque l'énergie est introduite dans un guide d'ondes, un champ électrique (champ E) est induit dans le centre de la paroi large « a ». Ce champ électrique est plus fort au centre du guide d'ondes et diminue dans la direction de la paroi étroite « b ». Il a une forme sinusoïdale vu en coupe. Un champ magnétique est également induit et, comme ce champ ne peut être maintenu verticalement sur un conducteur métallique, il prend la direction orthogonale.
Le champ électrique varie dans le temps selon la fréquence du signal et donne dans la direction longitudinale du guide d'ondes des maxima et des minima aux endroits correspondant à la moitié de la longueur d'onde. L’énergie à haute fréquence qui est introduite dans un guide d'onde, génère une onde électromagnétique transversale (mode TEM) dont les champs électrique et magnétique sont perpendiculaires les uns aux autres. Ces champs ne restent pas dans leur état respectif et se propagent ainsi dans les guides d’onde. Avec le temps, ils changent l'intensité et de polarité au rythme du signal d'entrée. Cette onde électromagnétique se propage dans le guide d'ondes à une vitesse proche de celle de la lumière (environ 300 millions de mètres par secondes). Leur interaction permet ainsi de transmettre l’énergie du signal d’entrée vers sa destination.

Figure 4 : Vu en coupe du champs électrique dans un guide d’ondes Mode TE10)
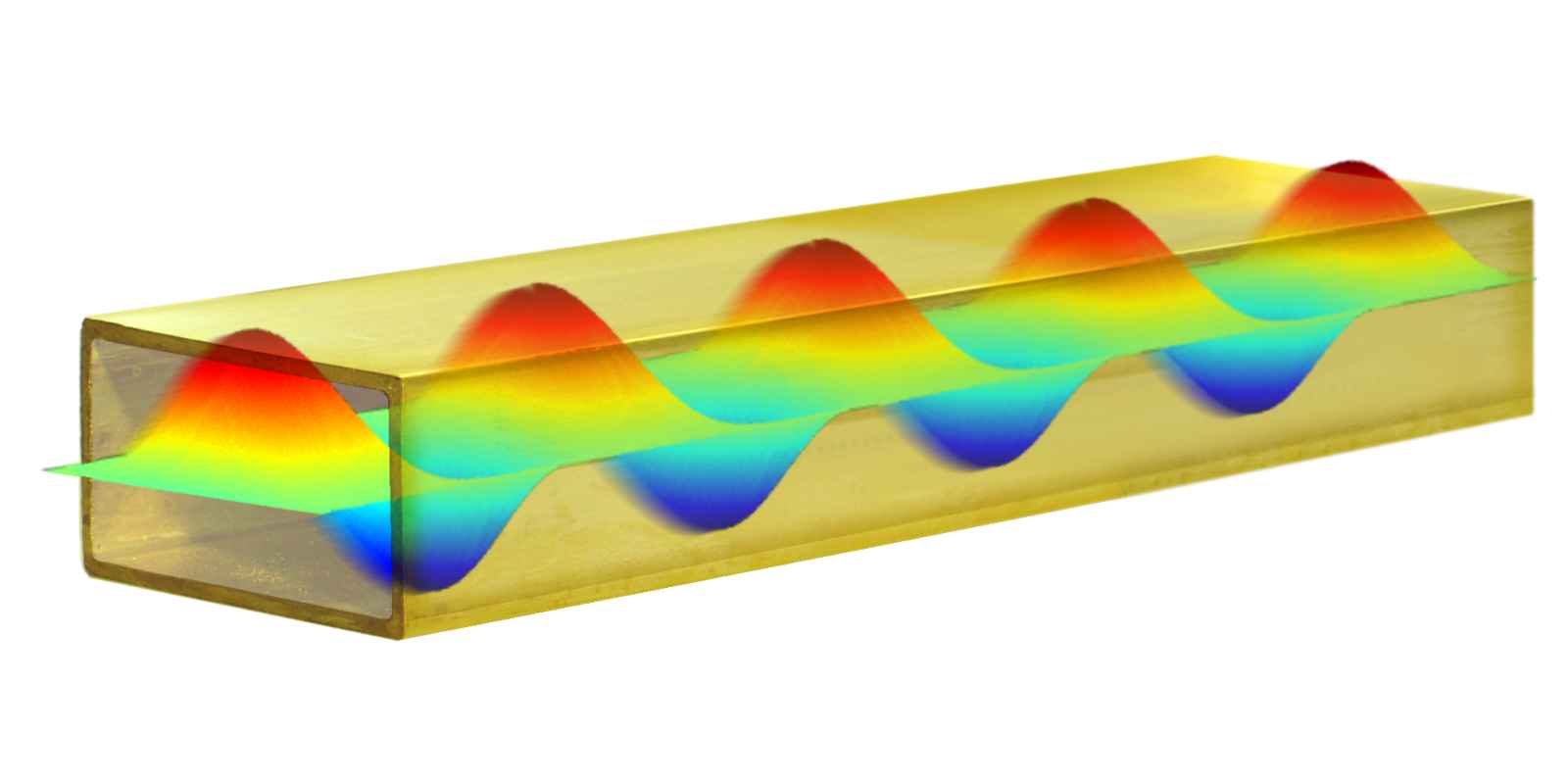
Figure 5 : Vue tridimensionnelle des champs électrique et magnétiques pour le mode TE₁₀ dans un guide de section rectangulaire.
Figure 5 : Vue tridimensionnelle des champs électrique et magnétiques pour le mode TE₁₀ dans un guide de section rectangulaire.
Älteres Bild nicht mehr in Großformat:
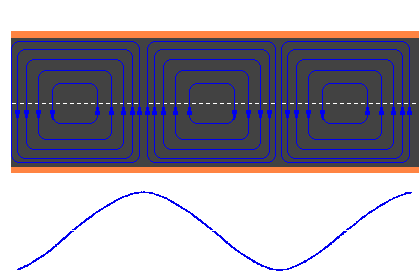
Figure 6 : H field in the waveguide (top view, snapshot)
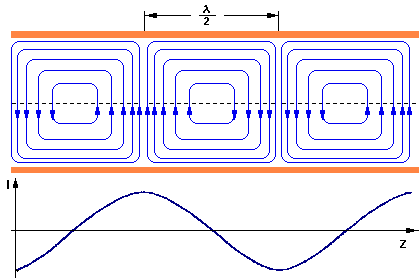
Figure 6 : H field in the waveguide (top view, snapshot)

Figure 6 : H field in the waveguide (top view, snapshot)
Les champs électriques et magnétiques changent d’intensité et de puissance façon permanente, mais ils sont toujours perpendiculaires les unes aux autres en chaque point du guide. Si le champ électrique est dans la direction de propagation, il est appelé en mode E ou onde de TM (transverse magnétique). Si le champ magnétique est dans la direction de propagation, il est appelé en mode H ou ondes TE (transverse électrique).
Guide d’onde
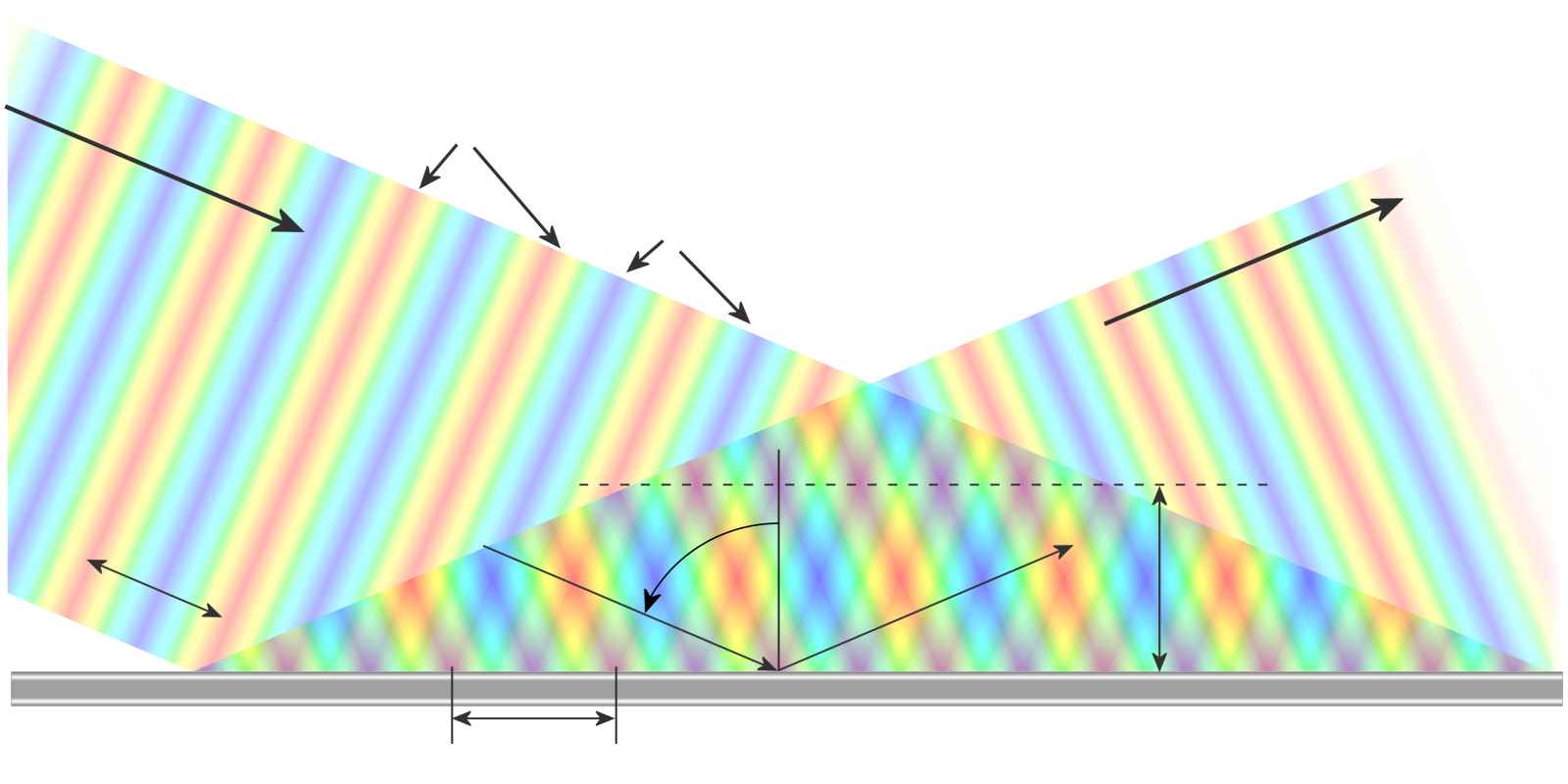
Figure 6 : Réflexion d’une onde arrivant à un angle oblique sur le mur métallique du guide.
Propagation par multiples réflexions
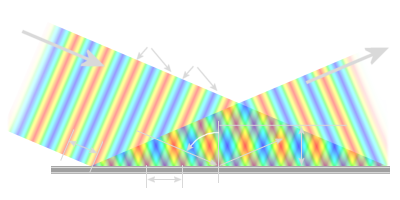
La propagation dans un guide d’ondes peut être expliquée en partie par l’optique géométrique et les propriétés des ondes en espace libre s’appliquent donc dans ce cas. Dans la figure 6, une onde plane de longueur d’onde λ0, avec un certain angle d’incidence (ici φ = 67°), est réfléchie par le mur métallique du guide. L’amplitude du champ électrique E, perpendiculaire au plan de l’onde, est indiquée par des couleurs différentes. La crête de l’onde (avec +Emax) est indiquée en rouge et le creux (avec −Emax) en bleu. Le vert donne le point de valeur nulle du champ.
Lors de la réflexion de l’onde, l’angle de réflexion est égal à celui d’incidence mais l’onde effectue un changement de phase de 180 degrés. L’onde incidente et celle réfléchie interfèrent entre elles à une certaine distance latérale et verticale du mur comme le montre la superposition des couleurs. À une distance donnée a :
| a = 0.5 | λ0 | (2) |
| cos φ |
Il y a complète annulation du champ E car les ligne rouges (front d’onde incidente) et bleues (front d’onde réfléchi) se superposent donnant une couleur magenta sur l’image (en fait la valeur du champ étant nulle, la couleur devrait être verte). Avec le déplacement des crêtes et creux de l’onde incidente, la position des points d’interférence se déplace constamment vers la droite.
En mettant un mur métallique à une distance « a » au-dessus du premier, sans changer rien d’autre, il y a réflexion totale interne de l’onde et formation de « paquets » d’onde qui se déplacent à la vitesse de phase, ou de groupe, vers la droite correspondant au comportement tridimensionnel de l’onde dans la figure 5. Les deux murs (celui tracé en bas et celui identifié par une ligne au-dessus) correspondent aux murs « b » dans un guide d’onde.
Avec ce graphique, il est également possible de déterminer que la propagation optimale dans un guide d’onde ne se produit que lorsque l’angle d’incidence est égal ou supérieur à l’écartement calculé par « a » dont la valeur dépend également de l’angle d’incidence φ et de la longueur λ0 d’onde utilisée.
Longueurs d’onde dans un guide d’ondes
En pratique, les valeurs maximales et minimales du champ E dans un guide d’onde sont le résultat des multiples interférences des ondes réfléchies par tous les murs. Les « paquets » se déplaçant vers la droite peuvent ainsi avoir une distance inter-maxima différente que celle en espace libre avec la même longueur d’onde λ0.
On calcule la différence inter-maxima avec :
| λh = | λ0 | (3) |
| sin φ |
Où la longueur d’onde de l’oscillation dans un guide d’onde (λh) est différente de celle en espace libre λ0. Comme l’angle d’incidence est difficile à mesurer, le rapport entre la longueur d’onde optimale et l’angle d’incidence de la formule 2 de l’extraire en espace libre. Par la suite, la longueur d’onde dans le guide d’onde peut être calculée en utilisant les formules 2 et 3 et donne la formule suivante :
.png) (4)
(4)
Le résultat est une vitesse de phase qui se propage comme une oscillation uniforme avec un facteur de sin φ plus élevé que la vitesse de la lumière. Conséquemment, la longueur d’onde λh dans le guide d’onde est souvent plus grande de manière significative que dans l’espace libre. Le transport d’énergie, et donc le changement local de E par une modulation de l’onde, se fait cependant à une vitesse plus petite que la vitesse de la lumière.

Figure 7 : Instantané des courants induits dans les murs du guide d’ondes par une onde TE₁₀. Cette configuration se déplace approximativement à la vitesse de la lumière dans la direction de propagation de l’onde.
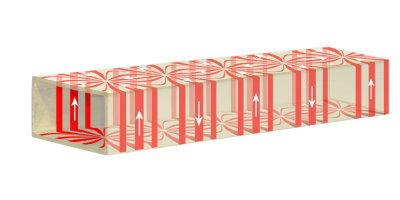
Figure 7 : Instantané des courants induits dans les murs du guide d’ondes par une onde TE₁₀. Cette configuration se déplace approximativement à la vitesse de la lumière dans la direction de propagation de l’onde.
Raisons de l’atténuation
L’atténuation dans un guide d’ondes est proportionnelle à la fréquence du signal. Même avec une fréquence de coupure, l’atténuation est importante mais atteint un minimum en augmentant la fréquence jusqu’à une certaine valeur, demeure ensuite presque constante, puis augmente à nouveau. Le facteur important pour avoir une bonne conductivité dans un guide rectangulaire est sa dimension « a » qui défini la fréquence de coupure. En effet, la longueur d’onde du signal doit être de dimension proche de celle de ce mur pour pouvoir induire un courant qui propagera l’onde dans celui-ci. Donc, plus la fréquence à transmettre est élevée, plus le mur « a » doit être petit et vise-et-versa.
L’atténuation des ondes est absorbée par les courants induits dans les murs. La figure 7 montre la distribution des ceux-ci dans le mur « a » avec une onde TE₁₀. Le flux passe du mur horizontal en bas vers celui en haut mais ce circuit se déplace dans le temps dans la direction de propagation de l’onde. La constante d’atténuation dans un mode de propagation donné peut être estimée en calculant l’intégrale de surface de la densité de courant dans le mur.
Ce courant n’est induit que dans la partie interne du guide d’ondes fait généralement de bronze poli, le mur interne doit donc avoir une excellente conductivité. Sa surface peut être plaquée argent (à partir de 40 GHz) ou or pour augmenter sa conductivité et les impuretés dues à la pollution vont de façon inverse augmenter son atténuation.
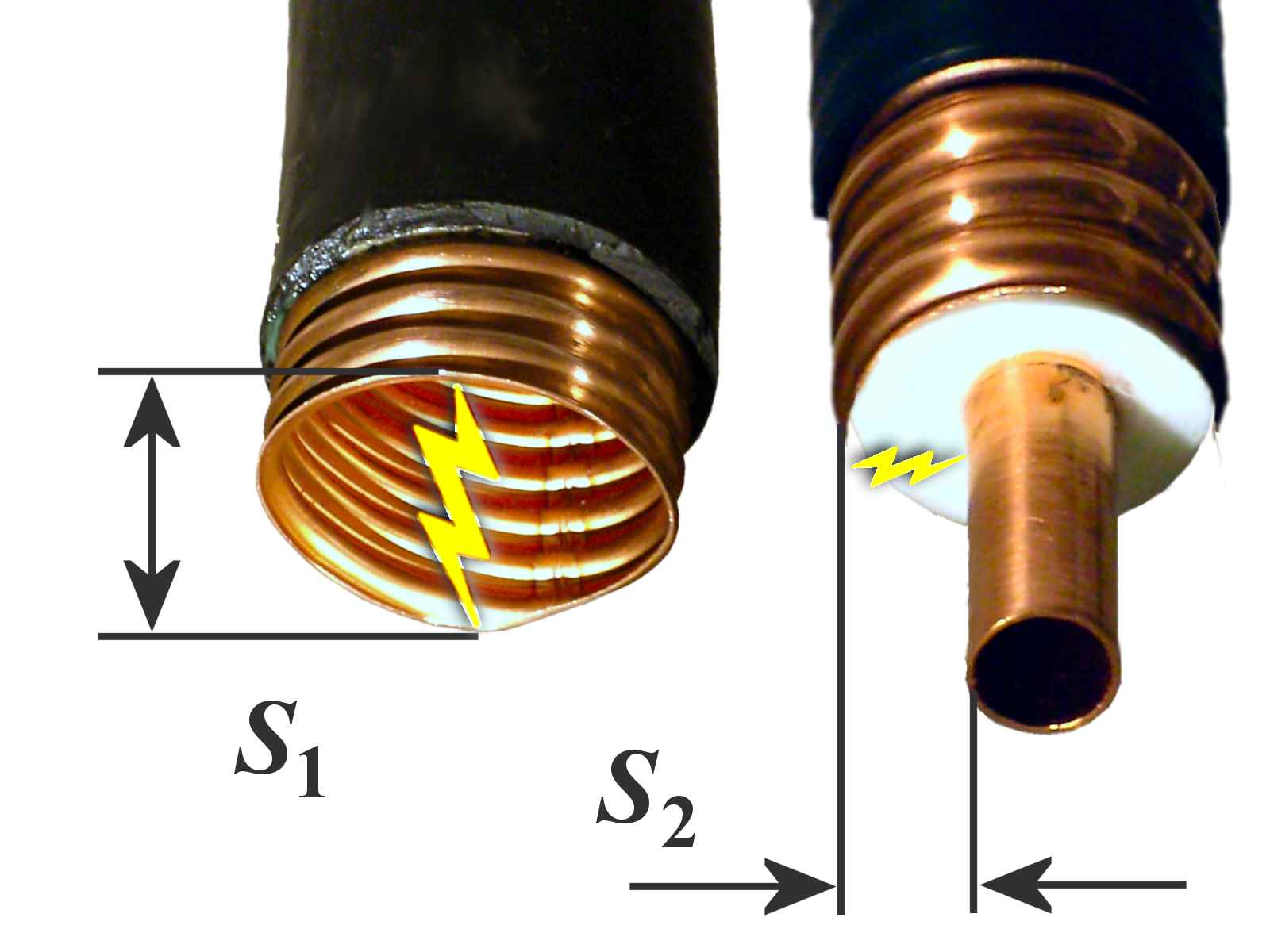
Figure 8 : Guide d’onde de section circulaire de diamètre semblable à câble coaxial mais dont la rigidité diélectrique est meilleure.

Figure 8 : Guide d’onde de section circulaire de diamètre semblable à câble coaxial mais dont la rigidité diélectrique est meilleure.
Rigidité diélectrique
La rigidité diélectrique est la valeur maximale d'un champ électrique que peut supporter l’isolant dans un guide d’onde sans décharge disruptive d’une paroi à l’autre. Elle est habituellement exprimée en kilovolts par millimètre (kV/mm) et dépend directement de l’espacement entre les parois à fréquence égale. Pour un guide d’ondes de section rectangulaire, cette distance dépend donc de la longueur du mur le plus court « b ». La rigidité dépend aussi de l’humidité de l’air contenu dans le guide. Pour améliorer ce facteur, les guides à haute puissance sont pressurisés avec de l’air déshumidifié. Si un endroit développe une fuite, l’air sec s’échappe mais la pression interne étant plus forte que celle de l’environnement, l’humidité externe ne peut pénétrer dans le guide.
Usages
Les guides d’ondes sont utilisés dans :
- Les transmetteurs de haute puissance ;
- Les équipements radars ;
- Les fours micro-ondes ;
- Les bloc-convertisseurs à faible bruit des antennes de réception des signaux de télévision.