Distance oblique
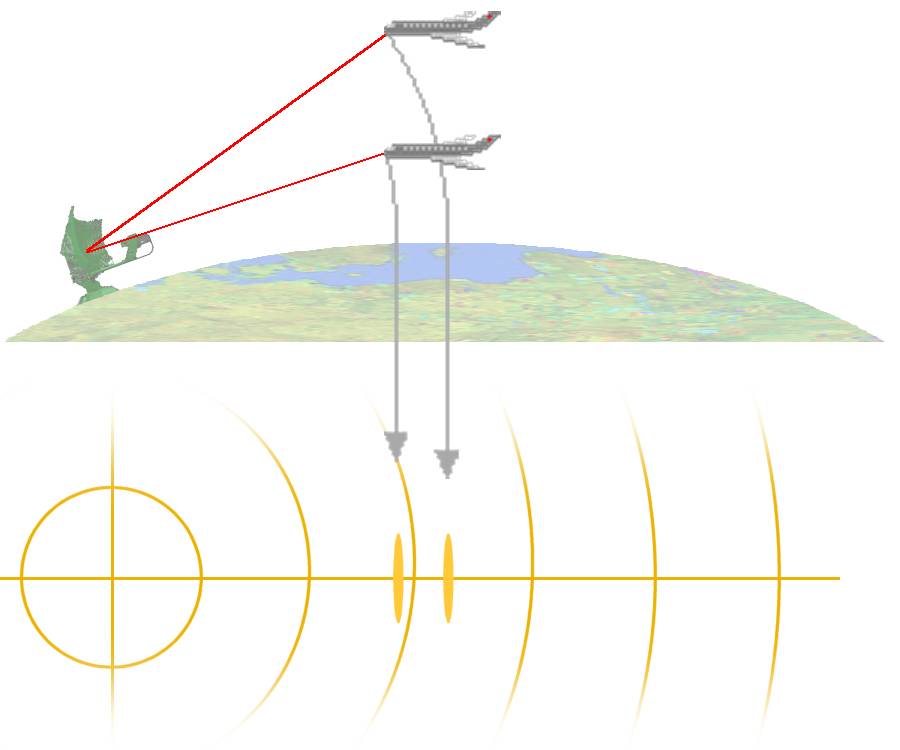
Figure 1 : Distance entre deux avions situés à des niveaux différents par rapport à un plan de référence tel que vu sur un PPI.
Figure 1 : Distance entre deux avions situés à des niveaux différents par rapport à un plan de référence tel que vu sur un PPI.
Distance oblique
Le radar mesure la distance radiale entre l’antenne et les cibles et ne tient pas compte de la courbure de la Terre. Cette distance est augmente avec l’altitude des cibles ce qui veut dire que deux avions situés à la même distance terrestre du radar, mais à des altitudes différentes, apparaissent à une distance différente sur l’affichage présenté à l’opérateur. C’est ce qu’on appelle la distance oblique.
Cette erreur de positionnement peut être corrigée par le logiciel de traitement des données du radar, comme dans le cas du RRP/ndash;117. Le logiciel doit contenir les divers paramètres de l’environnement autour du radar pour bien faire son calcul. Ces paramètres incluent le relief et des informations sur les conditions atmosphériques.
Des radars plus anciens en deux dimensions, comme le ASR-910 encore utilisé pour le trafic aérien, n’ont pas ce type de correction. L’opérateur doit donc être conscient qu’un avion situé à plus grande distance sur son affichage PPI peut être en réalité plus proche si son altitude est grande. Il doit donc faire une correction manuelle de la position de l’avion.
Calcul de la portée-aval

Figure 2 : Projection trigonométrique de la position d’un avion en ne considérant pas la courbure terrestre.
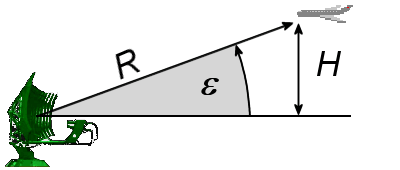
Figure 2 : Projection trigonométrique de la position d’un avion en ne considérant pas la courbure terrestre.

Figure 2 : Projection trigonométrique de la position d’un avion en ne considérant pas la courbure terrestre.
La distance entre le radar et la projection trigonométrique au sol de la position d’un avion est appelée « portée-aval ». Il est très important de savoir cette position car en général l’arrière du PPI comporte une carte géographique en arrière-plan qui permet de connaître les interactions possibles avec l’environnement.
Le calcul de la position topographique réelle est assez compliqué à obtenir cependant.
D’abord, la projection trigonométrique montrée dans la figure 2 pour une Terre plate se calcule:
Rtopogr. = R · cos ε
L’effet de la courbure de la Terre est évident dans la figure 3. La distance réelle au sol est différente à cause de :
- la distance oblique ;
- la hauteur réelle de la cible ;
- rayon de courbure de la Terre.

Figure 3 : Diagramme montrant la position réelle par rapport à la surface terrestre.
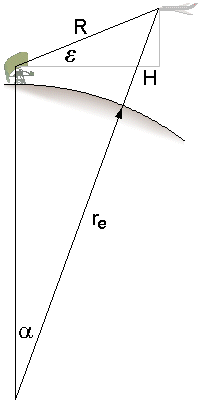
Figure 3 : Diagramme montrant la position réelle par rapport à la surface terrestre.

Figure 3 : Diagramme montrant la position réelle par rapport à la surface terrestre.
De la figure 3, on peut tirer la méthode de calcul de la position réelle.
En traçant un triangle entre le radar, le centre de la Terre et la cible, on peut utiliser la fonction trigonométrique suivante:
R2 = re2 + (re + H)2 - 2re(re + H) · cos α
(re est le rayon de la terre à cette endroit, H la hauteur de la cible et R la distance cible-radar).
En considérant que la terre est une sphère, l'arc de circonférence de la terre peut être calculé par le simple rapport entre
la circonférence totale de la terre et l'angle α:
360° · Rtopogr. = α · 2π re
Cette portion de la circonférence de la Terre est approximativement égale à la distance topographique, si on ne considère pas la réfraction. En pratique, cependant, la propagation des ondes électromagnétiques est soumise à la réfraction, c'est à dire que le faisceau d'ondes émis par le radar est un triangle dont les cotés sont courbés eux aussi, en fonction de :
- la longueur d'onde utilisée ;
- la pression barométrique ;
- la température de l'air ;
- le degré d'hygrométrie.
Donc la carte topographique superposé à l’affichage donne une erreur de positionnement si la correction n’est pas faite par le programme de traitement du signal radar. Ce défaut est toujours présent dans le cas d’un radar en deux dimensions qui ne peut obtenir la hauteur.
